题目内容
1. 如图,△ABD、△AEC都是等边三角形,BE和DC相交于点M.
如图,△ABD、△AEC都是等边三角形,BE和DC相交于点M.(1)求证:BE=DC.
(2)连接AM,试证明MA平分∠DME.
分析 (1)由等边三角形的性质得到AB=AD,AE=AC,∠DAB=∠EAC=60°,然后可证明∠DAC=∠BAE,接下来证明△DAC≌△BAE可得到DC=BE;
(2)过点A作AF⊥DC,AG⊥BE,垂足分别为F、G.首先证明△DAF≌△BAG,依据全等三角形的性质得到AF=AG,最后依据到角两边距离相等的点在角的平分线上.
解答 解:(1)∵△ABD、△AEC都是等边三角形,
∴AB=AD,AE=AC,∠DAB=∠EAC=60°.
∴∠DAC=∠BAE.
∵在△DAC和△BAE中$\left\{\begin{array}{l}{AD=AB}\\{∠DAC=∠BAE}\\{AC=AE}\end{array}\right.$,
∴△DAC≌△BAE.
∴DC=BE.
(2)过点A作AF⊥DC,AG⊥BE,垂足分别为F、G.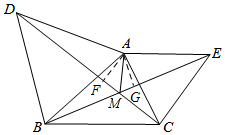
∵AF⊥DC,AG⊥BE,
∴∠DFA=∠BGA=90°.
∵△DAC≌△BAE,
∴∠ADC=∠ABE.
在△DAF和△BAG中$\left\{\begin{array}{l}{∠ADC=∠ABE}\\{∠DFA=∠BGA}\\{AD=AB}\end{array}\right.$,
∴△DAF≌△BAG.
∴AF=AG.
又∵AF⊥DC,AG⊥BE,
∴MA为∠DME的角平分线.
点评 本题主要考查的是等边三角形的性质、全等三角形的性质和判定、角平分线的性质,掌握本题辅助线的做法是解题的关键.

练习册系列答案
相关题目
12.下列各式中的大小关系成立的是( )
| A. | $-0.3<-\frac{1}{3}$ | B. | $-\frac{6}{5}>-\frac{7}{6}$ | C. | (-2)3>(-2)2 | D. | $-\frac{9}{10}>-\frac{10}{9}$ |
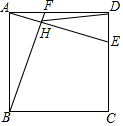 如图,在边长为2的正方形ABCD中,点E在边DC上运动,点F在边AD上运动,且DE=AF,AE,BF交于点H,连接DH,则DH的最小值为$\sqrt{5}-1$.
如图,在边长为2的正方形ABCD中,点E在边DC上运动,点F在边AD上运动,且DE=AF,AE,BF交于点H,连接DH,则DH的最小值为$\sqrt{5}-1$.
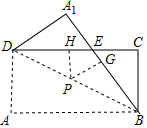 如图,四边形ABCD是长方形,将△ABD沿着BD翻折,点A的对应点为A1,BA1与CD交于点E,点P是线段DB(除去点D和点B)上任意一点,过点P分别作CD和BA1的 垂线,垂足为点G和点H,已知AB=8,AD=4,则PG+PH=4.
如图,四边形ABCD是长方形,将△ABD沿着BD翻折,点A的对应点为A1,BA1与CD交于点E,点P是线段DB(除去点D和点B)上任意一点,过点P分别作CD和BA1的 垂线,垂足为点G和点H,已知AB=8,AD=4,则PG+PH=4.