题目内容
4.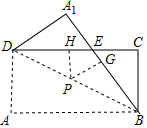 如图,四边形ABCD是长方形,将△ABD沿着BD翻折,点A的对应点为A1,BA1与CD交于点E,点P是线段DB(除去点D和点B)上任意一点,过点P分别作CD和BA1的 垂线,垂足为点G和点H,已知AB=8,AD=4,则PG+PH=4.
如图,四边形ABCD是长方形,将△ABD沿着BD翻折,点A的对应点为A1,BA1与CD交于点E,点P是线段DB(除去点D和点B)上任意一点,过点P分别作CD和BA1的 垂线,垂足为点G和点H,已知AB=8,AD=4,则PG+PH=4.
分析 连接PE,根据翻转变换的性质得到DE=BE,设CE=x,根据勾股定理列出方程,求出x,根据三角形的面积公式计算即可.
解答 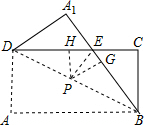 解:连接PE,
解:连接PE,
由题意可得,AD=BC=DA1,∠A1=∠C=90°,∠DEA1=∠BEC,
∴△BEC≌△DEA1,
∴DE=BE,
设CE=x,则DE=8-x.
由勾股定理得,(8-x)2=16+x2,
解得x=3,
∴CE=3,DE=BE=5,
∴△DEB的面积为:$\frac{1}{2}$×5×4=10,
即$\frac{1}{2}$×5×PH+$\frac{1}{2}$×5×PG=10,
∴PG+PH=4,
故答案为:4.
点评 本题考查的是翻转变换的性质、勾股定理的应用,翻转变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
19.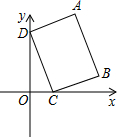 如图,在平面直角坐标系中,长方形ABCD的顶点C、D分别在x轴、y轴的正半轴上,顶点A、B在第一象限,其中顶点B的坐标是(3,1),顶点D的坐标是(0,3),线段AB=$\sqrt{10}$,则顶点A的坐标是( )
如图,在平面直角坐标系中,长方形ABCD的顶点C、D分别在x轴、y轴的正半轴上,顶点A、B在第一象限,其中顶点B的坐标是(3,1),顶点D的坐标是(0,3),线段AB=$\sqrt{10}$,则顶点A的坐标是( )
 如图,在平面直角坐标系中,长方形ABCD的顶点C、D分别在x轴、y轴的正半轴上,顶点A、B在第一象限,其中顶点B的坐标是(3,1),顶点D的坐标是(0,3),线段AB=$\sqrt{10}$,则顶点A的坐标是( )
如图,在平面直角坐标系中,长方形ABCD的顶点C、D分别在x轴、y轴的正半轴上,顶点A、B在第一象限,其中顶点B的坐标是(3,1),顶点D的坐标是(0,3),线段AB=$\sqrt{10}$,则顶点A的坐标是( )| A. | (2,4) | B. | ($\frac{5}{2}$,4) | C. | (3,4) | D. | (2,5) |
14.中国月球探测工程的“嫦娥一号”发射升空飞向月球,已知地球距离月球表面约为384 000千米,那么这个距离用科学记数法表示为( )
| A. | 3.84×l04 千米 | B. | 3.84×l05千米 | C. | 3.84×l06千米 | D. | 38.4×l04 千米 |
 如图,△ABD、△AEC都是等边三角形,BE和DC相交于点M.
如图,△ABD、△AEC都是等边三角形,BE和DC相交于点M.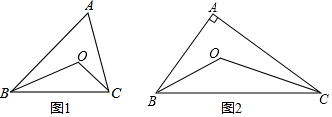
 如图,已知点A、C、F、E在同一直线上,△ABC是等边三角形,且CD=CE,EF=EG,则∠F=15度.
如图,已知点A、C、F、E在同一直线上,△ABC是等边三角形,且CD=CE,EF=EG,则∠F=15度. 如图,在△ABC中,∠BAC=90°,AB=AC,BD平分∠ABC时
如图,在△ABC中,∠BAC=90°,AB=AC,BD平分∠ABC时