题目内容
19.若关于x的一元二次方程x2-4x+k=0有两个不相等的实数根,则k的值可以是3(写出一个即可)分析 先根据根的判别式求出k的范围,再在范围内取一个符合的数即可.
解答 解:∵关于x的一元二次方程x2-4x+k=0有两个不相等的实数根,
∴△=(-4)2-4×1×k=16-4k>0,
解得k<4,
取k=3,
故答案为:3.
点评 本题考查了根的判别式,能根据根的判别式的内容得出关于k的不等式是解此题的关键.

练习册系列答案
相关题目
9.已知$\sqrt{x+y-1}$+$\sqrt{x-y+3}$=0,则(x+y)2016=( )
| A. | 22016 | B. | -1 | C. | 1 | D. | -22016 |
11.为了提高学生的汉字书写能力,某学校连续举办了几届汉字听写大赛,2017年,经过层层选拔,确定了参加决赛的选手,决赛的比赛规则是每正确听写出一个汉字得2分,满分是100分,下面是根据测试成绩绘制出的2017年的不完整的频数分布表,频数分布直方图和频数分布扇形图.
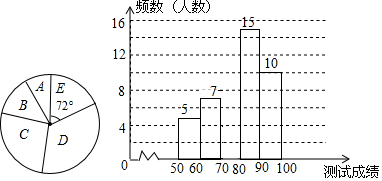
请结合图表完成下列各题:
(1)求表中a的值并把频数分布直方图补充完整;
(2)利用频数分布进行估算,今年参加决赛的学生的平均成绩能否达到70分?
(3)为了查明A类学生成绩较差的原因,学校决定对A类学生学习汉字的能力进行研究,想从其中的3名女生和2名男生中选出两人,正好选中一名男生和一名女生的概率是多少?
| 类别 | 成绩x分 | 频数(人数) |
| A | 50≤x<60 | 5 |
| B | 60≤x<70 | 7 |
| C | 70≤x<80 | a |
| D | 80≤x<90 | 15 |
| E | 90≤x<100 | 10 |

请结合图表完成下列各题:
(1)求表中a的值并把频数分布直方图补充完整;
(2)利用频数分布进行估算,今年参加决赛的学生的平均成绩能否达到70分?
(3)为了查明A类学生成绩较差的原因,学校决定对A类学生学习汉字的能力进行研究,想从其中的3名女生和2名男生中选出两人,正好选中一名男生和一名女生的概率是多少?
8.如图,图中所有的梯形一组底角度数都是60°,上底长度是1,下底长度是2,两腰长度是1,点,P从点O出发,每秒1个单位长度沿O-A-B-C-D-E-F-G-H…折线方向移动,确定第2016秒时,点P的坐标为( )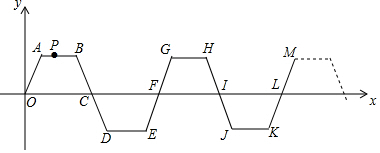

| A. | (1342,0) | B. | (1343,0) | C. | (1344,0) | D. | (1345,0) |
9.380亿用科学记数法表示为( )
| A. | 38×109 | B. | 0.38×1013 | C. | 3.8×1011 | D. | 3.8×1010 |
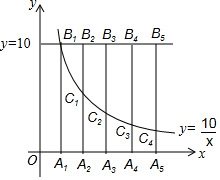 如图,直线y=10与反比例函数y=$\frac{10}{x}$( x>0)图象交于点B1,作A1B1⊥x轴,垂足为A1,在A1右侧依次取连续整数点,(横坐标为整数)A2,A3,A4,A5,过这些整数点分别作y轴的平行线交直线y=10于B2,B3,B4,B5,交反比例函数y=$\frac{10}{x}$(x>0)图象于点C1,C2,C3,C4.若B2C1=aA2C1,B3C2=bA3C2,B4C3=cA4C3,B5C4=dA5C4,则a+b+c+d的值为.
如图,直线y=10与反比例函数y=$\frac{10}{x}$( x>0)图象交于点B1,作A1B1⊥x轴,垂足为A1,在A1右侧依次取连续整数点,(横坐标为整数)A2,A3,A4,A5,过这些整数点分别作y轴的平行线交直线y=10于B2,B3,B4,B5,交反比例函数y=$\frac{10}{x}$(x>0)图象于点C1,C2,C3,C4.若B2C1=aA2C1,B3C2=bA3C2,B4C3=cA4C3,B5C4=dA5C4,则a+b+c+d的值为. 某校举办一项小制作评比,作品上交时限为5月1日至30日,组委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1.第三组的频数是12.请你回答:
某校举办一项小制作评比,作品上交时限为5月1日至30日,组委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1.第三组的频数是12.请你回答: