题目内容
10.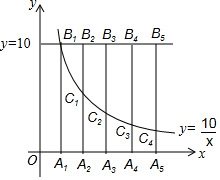 如图,直线y=10与反比例函数y=$\frac{10}{x}$( x>0)图象交于点B1,作A1B1⊥x轴,垂足为A1,在A1右侧依次取连续整数点,(横坐标为整数)A2,A3,A4,A5,过这些整数点分别作y轴的平行线交直线y=10于B2,B3,B4,B5,交反比例函数y=$\frac{10}{x}$(x>0)图象于点C1,C2,C3,C4.若B2C1=aA2C1,B3C2=bA3C2,B4C3=cA4C3,B5C4=dA5C4,则a+b+c+d的值为.
如图,直线y=10与反比例函数y=$\frac{10}{x}$( x>0)图象交于点B1,作A1B1⊥x轴,垂足为A1,在A1右侧依次取连续整数点,(横坐标为整数)A2,A3,A4,A5,过这些整数点分别作y轴的平行线交直线y=10于B2,B3,B4,B5,交反比例函数y=$\frac{10}{x}$(x>0)图象于点C1,C2,C3,C4.若B2C1=aA2C1,B3C2=bA3C2,B4C3=cA4C3,B5C4=dA5C4,则a+b+c+d的值为.| A. | 10 | B. | 8 | C. | 6 | D. | 5 |
分析 根据A2(2,0),C1(2,5),B2(2,10),可得B2C1=10-5=5,A2C1=5,进而得到a=1,同理可得b,c,d的值,即可得到a+b+c+d的值.
解答 解:反比例函数y=$\frac{10}{x}$中,令y=10,则x=1,
∴B1(1,10),A1(1,0),
在A1右侧依次取连续整数点,可得A1(1,0),A2(2,0),A3(3,0),A4(4,0),A5(5,0),
过这些整数点分别作y轴的平行线,可得B2(2,10),B3(3,10),B4(4,10),B5(5,10),
反比例函数y=$\frac{10}{x}$中,
令x=2,则y=5,即C1(2,5);
令x=3,则y=$\frac{10}{3}$,即C2(3,$\frac{10}{3}$);
令x=4,则y=$\frac{5}{2}$,即C3(4,$\frac{5}{2}$);
令x=5,则y=2,即C4(5,2);
∴B2C1=10-5=5,A2C1=5,即a=1,
B3C2=10-$\frac{10}{3}$=$\frac{20}{3}$,A3C2=$\frac{10}{3}$,即b=2,
B4C3=10-$\frac{5}{2}$=$\frac{15}{2}$,A4C3=$\frac{5}{2}$,即c=3,
B5C4=10-2=8,A5C4=2,即d=4,
∴a+b+c+d的值为10,
故选:A.
点评 本题主要考查了反比例函数与一次函数交点问题,解题时注意:反比例函数与一次函数交点的坐标同时满足反比例函数与一次函数的解析式.

练习册系列答案
相关题目
18.某服装专卖店销售的A款品牌西服去年销售总额为50000元,今年该款西服每件售价比去年便宜400元,若售出的件数相同,则该款西服销售总额将比去年降低20%,求今年该款西服的每件售价.若设今年该款西服的每件售价为x元,那么可列方程为( )
| A. | $\frac{50000}{x+400}$=$\frac{50000×(1-20%)}{x}$ | B. | $\frac{50000}{x}$=$\frac{50000×(1-20%)}{x+400}$ | ||
| C. | $\frac{50000}{x-400}$=$\frac{50000×(1-20%)}{x}$ | D. | $\frac{50000}{x}=\frac{50000×(1-20%)}{x-400}$ |
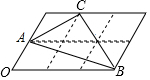 如图,6个形状、大小完全相同的菱形组成网格,已知菱形的一个角∠O为60°,A,B,C都在格点上,则tan∠ABC的值为$\frac{\sqrt{3}}{2}$.
如图,6个形状、大小完全相同的菱形组成网格,已知菱形的一个角∠O为60°,A,B,C都在格点上,则tan∠ABC的值为$\frac{\sqrt{3}}{2}$.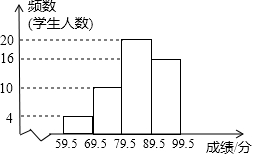 为增强学生环保意识,某中学组织全校2000名学生参加环保知识大赛,比赛成绩均为整数.从中抽取部分同学的成绩进行统计,并绘制成如图统计图.
为增强学生环保意识,某中学组织全校2000名学生参加环保知识大赛,比赛成绩均为整数.从中抽取部分同学的成绩进行统计,并绘制成如图统计图.