题目内容
4. 如图,在△ABC中,PA,PB分别平分∠BAC和∠ABC,PH⊥AB,垂足为H,已知∠C=90°,BC=3,AC=4,求PH的长.
如图,在△ABC中,PA,PB分别平分∠BAC和∠ABC,PH⊥AB,垂足为H,已知∠C=90°,BC=3,AC=4,求PH的长.
分析 连接PC,作PE⊥AC于E,PF⊥BC于F,根据勾股定理求出AB的长,根据角平分线的性质得到PE=PF=PH,根据三角形面积公式求出答案.
解答 解:连接PC,作PE⊥AC于E,PF⊥BC于F,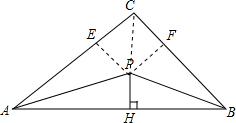
∵∠C=90°,BC=3,AC=4,
∴AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=5,
∵PA,PB分别平分∠BAC和∠ABC,PH⊥AB,PE⊥AC,PF⊥BC,
∴PE=PF=PH,
$\frac{1}{2}$×AC×PE+$\frac{1}{2}$×BC×PF+$\frac{1}{2}$×AB×PH=$\frac{1}{2}$×AC×BC,
解得,PH=1.
点评 本题考查的是角平分线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
相关题目
 如图所示,已知△ABC中,AB=AC,∠BAD=30°,AD=AE,求∠EDC的度数.
如图所示,已知△ABC中,AB=AC,∠BAD=30°,AD=AE,求∠EDC的度数.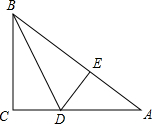 如图,在△ABC中,∠C=90°,点D、E分别在边AC、AB上,BD平分∠ABC,DE⊥AB,AE=8,sinA=$\frac{3}{5}$.
如图,在△ABC中,∠C=90°,点D、E分别在边AC、AB上,BD平分∠ABC,DE⊥AB,AE=8,sinA=$\frac{3}{5}$. 如图是一个简单的数值运算程序,当输入的x的值为-2时,输出的值为9.
如图是一个简单的数值运算程序,当输入的x的值为-2时,输出的值为9.