题目内容
5.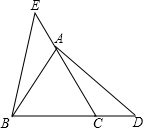 已知,如图,等边△ABC中,点D为BC延长线上一点,点E为CA延长线上一点,且AE=DC,求证:AD=BE.
已知,如图,等边△ABC中,点D为BC延长线上一点,点E为CA延长线上一点,且AE=DC,求证:AD=BE.
分析 先根据等边△ABC中,AB=CA,∠BAC=∠ACB=60°,得出∠EAB=∠DCA=120°,再根据SAS即可判定△EAB≌△DCA,进而得出结论.
解答 证明:在等边△ABC中,AB=CA,∠BAC=∠ACB=60°,
∴∠EAB=∠DCA=120°.
在△EAB和△DCA中,
$\left\{\begin{array}{l}{AE=DC}\\{∠EAB=∠DCA}\\{AB=CA}\end{array}\right.$,
∴△EAB≌△DCA(SAS),
∴AD=BE.
点评 本题主要考查了等边三角形的性质以及全等三角形的判定与性质的运用,解题时注意:两边及其夹角分别对应相等的两个三角形全等.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
16.若圆锥的底面半径为3,母线长为5,则这个圆锥的侧面积为( )
| A. | 6π | B. | 8π | C. | 15π | D. | 30π |
10. 如图,在平面直角坐标系中,反比例函数y=$\frac{3}{x}$(x>0)的图象经过A、B两点,菱形ABCD在第一象限内,边BC于x轴平行.若A、B两点的纵坐标分别为3和1,则菱形ABCD的面积为( )
如图,在平面直角坐标系中,反比例函数y=$\frac{3}{x}$(x>0)的图象经过A、B两点,菱形ABCD在第一象限内,边BC于x轴平行.若A、B两点的纵坐标分别为3和1,则菱形ABCD的面积为( )
 如图,在平面直角坐标系中,反比例函数y=$\frac{3}{x}$(x>0)的图象经过A、B两点,菱形ABCD在第一象限内,边BC于x轴平行.若A、B两点的纵坐标分别为3和1,则菱形ABCD的面积为( )
如图,在平面直角坐标系中,反比例函数y=$\frac{3}{x}$(x>0)的图象经过A、B两点,菱形ABCD在第一象限内,边BC于x轴平行.若A、B两点的纵坐标分别为3和1,则菱形ABCD的面积为( )| A. | 2 | B. | 4 | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
17. 从甲、乙两名同学中选拔一人参加“中华好诗词”大赛,在相同的测试条件下,对两人进行了五次模拟,并对成绩(单位:分)进行了整理,计算出$\overline{x甲}$=83分,$\overline{x乙}$=82分,绘制成如下尚不完整的统计图表.
从甲、乙两名同学中选拔一人参加“中华好诗词”大赛,在相同的测试条件下,对两人进行了五次模拟,并对成绩(单位:分)进行了整理,计算出$\overline{x甲}$=83分,$\overline{x乙}$=82分,绘制成如下尚不完整的统计图表.
甲、乙两人模拟成绩统计表
根据以上信息,回答下列问题:
(1)a=85
(2)请完成图中表示甲成绩变化情况的折线.
(3)经计算S甲2=6,S乙2=42,综合分析,你认为选拔谁参加比赛更合适,说明理由.
(4)如果分别从甲、乙两人5次的成绩中各随机抽取一次成绩进行分析,求抽到的两个人的成绩都大于82分的概率.
 从甲、乙两名同学中选拔一人参加“中华好诗词”大赛,在相同的测试条件下,对两人进行了五次模拟,并对成绩(单位:分)进行了整理,计算出$\overline{x甲}$=83分,$\overline{x乙}$=82分,绘制成如下尚不完整的统计图表.
从甲、乙两名同学中选拔一人参加“中华好诗词”大赛,在相同的测试条件下,对两人进行了五次模拟,并对成绩(单位:分)进行了整理,计算出$\overline{x甲}$=83分,$\overline{x乙}$=82分,绘制成如下尚不完整的统计图表.甲、乙两人模拟成绩统计表
| ① | ② | ③ | ④ | ⑤ | |
| 甲成绩/分 | 79 | 86 | 82 | a | 83 |
| 乙成绩/分 | 88 | 79 | 90 | 81 | 72 |
(1)a=85
(2)请完成图中表示甲成绩变化情况的折线.
(3)经计算S甲2=6,S乙2=42,综合分析,你认为选拔谁参加比赛更合适,说明理由.
(4)如果分别从甲、乙两人5次的成绩中各随机抽取一次成绩进行分析,求抽到的两个人的成绩都大于82分的概率.
 如图,?ABCD中,AD=2AB,点E在BC边上,且CE=$\frac{1}{4}$AD,F为BD的中点,连接EF.
如图,?ABCD中,AD=2AB,点E在BC边上,且CE=$\frac{1}{4}$AD,F为BD的中点,连接EF.