题目内容
15. 如图,△ABC中,∠B=∠C,∠3=∠4,∠1=44°,求∠2的度数.
如图,△ABC中,∠B=∠C,∠3=∠4,∠1=44°,求∠2的度数.
分析 根据三角形的外角的性质得到∠2+∠3=∠1+∠B,∠4=∠2+∠C,等量代换得到∠2+∠4=∠1+∠C,于是得到∠2=$\frac{1}{2}$∠1,即可得到结论.
解答 解:∵∠2+∠3=∠1+∠B,
∵∠B=∠C,∠3=∠4,
∵∠4=∠2+∠C,
∴∠2+∠4=∠1+∠C,
即∠2+∠2+∠C=∠1+∠C,
∴∠2=$\frac{1}{2}$∠1,
∵∠1=44°,
∴∠2=22°.
点评 本题考查了三角形的内角和,三角形的外角的性质,熟练掌握三角形的内角和是解题的关键.

练习册系列答案
相关题目
10.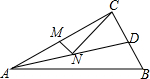 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,AD平分∠CAB交BC于点D,点M,N分别是AC和AD边上的动点,则MN+NC的最小值为( )
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,AD平分∠CAB交BC于点D,点M,N分别是AC和AD边上的动点,则MN+NC的最小值为( )
 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,AD平分∠CAB交BC于点D,点M,N分别是AC和AD边上的动点,则MN+NC的最小值为( )
如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,AD平分∠CAB交BC于点D,点M,N分别是AC和AD边上的动点,则MN+NC的最小值为( )| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | $\frac{12}{5}$ |
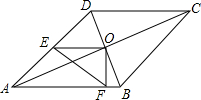 如图,在?ABCD中,对角线AC、BD相交于点O,点E、F分别是边AD、AB上的点,连结OE、OF、EF.若AB=7,BC=5$\sqrt{2}$,∠DAB=45°,则△OEF周长的最小值是$\frac{13\sqrt{2}}{2}$.
如图,在?ABCD中,对角线AC、BD相交于点O,点E、F分别是边AD、AB上的点,连结OE、OF、EF.若AB=7,BC=5$\sqrt{2}$,∠DAB=45°,则△OEF周长的最小值是$\frac{13\sqrt{2}}{2}$.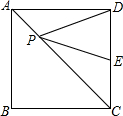 正方形ABCD中,点P是对角线AC上的动点,点E是CD的中点,AB=2,求PD+PE的最小值.
正方形ABCD中,点P是对角线AC上的动点,点E是CD的中点,AB=2,求PD+PE的最小值.