题目内容
4.已知y关于x的函数y=(k-1)x2-2kx+k+2,若该函数图象与x轴有两个交点,且k2+k=2,求k的值.分析 根据k2-k=2及k的范围,确定出k的值即可.
解答 解:由函数与x轴有两个交点,得
△=4k2-4(k-1)(k+2),且k-1≠0,
解得,k<2且k≠1,
k2+k=2变形得:(k+2)(k-1)=0,
解得:k=-2或k=1(不合题意,舍去),
则k的值为-2.
点评 此题考查了抛物线与x轴的交点,以及二次函数图象与性质,熟练掌握二次函数的图象与性质是解本题的关键.

练习册系列答案
相关题目
16. 如图所示,同位角共有( )对.
如图所示,同位角共有( )对.
 如图所示,同位角共有( )对.
如图所示,同位角共有( )对.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
13.下面的图案是由一个图形经过多次轴对称变换得到的,在这些对称轴中,共有平行线( )

| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
 如图,△ABC中,∠B=∠C,∠3=∠4,∠1=44°,求∠2的度数.
如图,△ABC中,∠B=∠C,∠3=∠4,∠1=44°,求∠2的度数. 如图,一次函数y=$\frac{\sqrt{3}}{3}$x+b的图象与x轴相交于点A(5$\sqrt{3}$,0),与y轴相交于点B
如图,一次函数y=$\frac{\sqrt{3}}{3}$x+b的图象与x轴相交于点A(5$\sqrt{3}$,0),与y轴相交于点B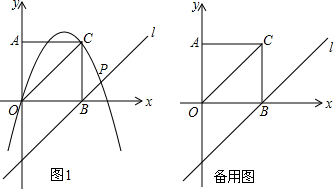
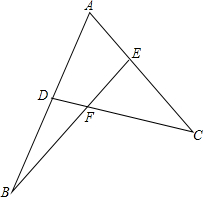 如图:∠ADC+∠AEB=180°,AB=k•AC,判断BE与CD的关系,并加以证明.
如图:∠ADC+∠AEB=180°,AB=k•AC,判断BE与CD的关系,并加以证明.