题目内容
12.已知$\frac{x}{2}$=$\frac{y}{3}$=$\frac{Z}{5}$ 求:①$\frac{2x+3y+z}{5z}$=$\frac{18}{25}$;
②当x+y+z=5时,x=1,y=$\frac{3}{2}$,z=$\frac{5}{2}$.
分析 ①利用已知比例式$\frac{x}{2}$=$\frac{y}{3}$=$\frac{Z}{5}$,用一个未知数表示出x,y,z,进而求出即可;
②利用①中关系结合x+y+z=5,求出即可.
解答 解:①∵$\frac{x}{2}$=$\frac{y}{3}$=$\frac{Z}{5}$,
∴设x=2a,y=3a,z=5a,
∴$\frac{2x+3y+z}{5z}$=$\frac{2×2a+3×3a+5a}{5×5a}$=$\frac{18}{25}$;
故答案为:$\frac{18}{25}$;
②∵$\frac{x}{2}$=$\frac{y}{3}$=$\frac{Z}{5}$,
∴设x=2a,y=3a,z=5a,
当x+y+z=5时,2a+3a+5a=5,
解得:a=$\frac{1}{2}$,
故x=1,y=$\frac{3}{2}$,z=$\frac{5}{2}$.
故答案为:1,$\frac{3}{2}$,$\frac{5}{2}$.
点评 此题主要考查了比例的性质,正确利用比例的性质将已知变形是解题关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
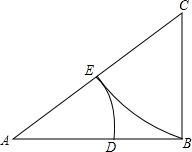 已知小强将线段AB黄金分割(点D为黄金分割点)所作的图形如图所示.请你回答:
已知小强将线段AB黄金分割(点D为黄金分割点)所作的图形如图所示.请你回答: △ABC中,D在BC上,且AB=AC=BD,∠1=30°,求∠2的度数.
△ABC中,D在BC上,且AB=AC=BD,∠1=30°,求∠2的度数. 如图,△ABC中,∠B=∠C,∠3=∠4,∠1=44°,求∠2的度数.
如图,△ABC中,∠B=∠C,∠3=∠4,∠1=44°,求∠2的度数.