题目内容
2.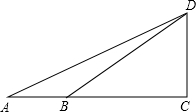 小明准备用所学数学知识测量广场上旗杆CD的高度,如图所示,在底面A处测得顶端的仰角为25.5°,在B处测得仰角为36.9°,已知点A、B、C在同一直线上,量得AB=10米.求旗杆的高度.(结果保留一位小数,参考数据:sin25.5°≈0.43,cos25.5°≈0.90,tan25.5°≈0.48;sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75.)
小明准备用所学数学知识测量广场上旗杆CD的高度,如图所示,在底面A处测得顶端的仰角为25.5°,在B处测得仰角为36.9°,已知点A、B、C在同一直线上,量得AB=10米.求旗杆的高度.(结果保留一位小数,参考数据:sin25.5°≈0.43,cos25.5°≈0.90,tan25.5°≈0.48;sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75.)
分析 设CD=x米,根据正切的概念用x表示出AC、BC,根据题意列出方程,解方程即可.
解答 解:设CD=x米,
在Rt△ADC中,AC=$\frac{CD}{tan∠A}$=$\frac{x}{tan22.5°}$,
在Rt△BDC中,BC=$\frac{CD}{tan∠DBC}$=$\frac{x}{tan36.9°}$,
∵AC-BC=AB,
∴$\frac{x}{0.48}$-$\frac{x}{0.75}$=10,
解得x≈13.3.
答:旗杆的高度为13.3米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
相关题目
12.已知1,2,3,4,5的方差是2,则101,102,103,104,105的方差是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
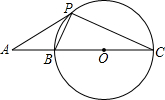 如图,点A、B、C在同一条直线上,点P在以BC为直径的⊙O上,连结PA、PB、PC,AB=BP=$\frac{1}{2}BC$.
如图,点A、B、C在同一条直线上,点P在以BC为直径的⊙O上,连结PA、PB、PC,AB=BP=$\frac{1}{2}BC$.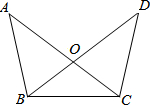 如图,已知∠ABO=∠DCO,OB=OC,求证:△ABC≌△DCB.
如图,已知∠ABO=∠DCO,OB=OC,求证:△ABC≌△DCB.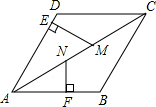 如图,在菱形ABCD中,点M、N在AC上,ME⊥AD,NF⊥AB,若NF=NM=2,ME=3,则AM=6.
如图,在菱形ABCD中,点M、N在AC上,ME⊥AD,NF⊥AB,若NF=NM=2,ME=3,则AM=6.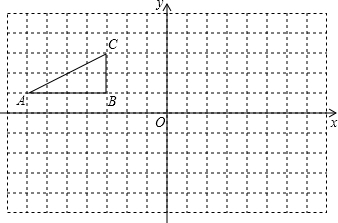
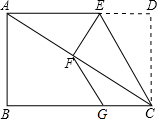 如图,已知点E是矩形一边AD上的一点,沿CE折叠矩形使点D落在对角线AC上的点F处,点G为BC上一点,且CG=DE,连FG.
如图,已知点E是矩形一边AD上的一点,沿CE折叠矩形使点D落在对角线AC上的点F处,点G为BC上一点,且CG=DE,连FG.