题目内容
10.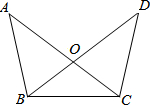 如图,已知∠ABO=∠DCO,OB=OC,求证:△ABC≌△DCB.
如图,已知∠ABO=∠DCO,OB=OC,求证:△ABC≌△DCB.
分析 根据ASA推出△ABO≌△DCO,根据全等三角形的性质得出∠A=∠D,求出∠ABC=∠DCB,根据AAS推出即可.
解答 证明:∵在△ABO和△DCO中
$\left\{\begin{array}{l}{∠ABO=∠DCO}\\{BO=CO}\\{∠AOB=∠DOC}\end{array}\right.$
∴△ABO≌△DCO(ASA),
∴∠A=∠D,
∵OB=OC,
∴∠OBC=∠OCB,
∵∠ABO=∠DCO,
∴∠ABO+∠OBC=∠DCO+∠OCB,
即∠ABC=∠DCB,
在△ABC和△DCB中,
$\left\{\begin{array}{l}{∠A=∠D}\\{∠ABC=∠DCB}\\{BC=BC}\end{array}\right.$
∴△ABC≌△DCB(AAS).
点评 本题考查了全等三角形的判定定理、性质定理和等腰三角形的性质的应用,能综合运用定理进行推理是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,符合SSA和AAA不能推出两三角形全等.

练习册系列答案
相关题目
1.下列运算正确的是( )
| A. | $\sqrt{2}+\sqrt{3}$=$\sqrt{5}$ | B. | 4x2y-x2y=4 | C. | a3•a4=a12 | D. | (a2b)3=a6b3 |
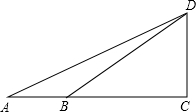 小明准备用所学数学知识测量广场上旗杆CD的高度,如图所示,在底面A处测得顶端的仰角为25.5°,在B处测得仰角为36.9°,已知点A、B、C在同一直线上,量得AB=10米.求旗杆的高度.(结果保留一位小数,参考数据:sin25.5°≈0.43,cos25.5°≈0.90,tan25.5°≈0.48;sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75.)
小明准备用所学数学知识测量广场上旗杆CD的高度,如图所示,在底面A处测得顶端的仰角为25.5°,在B处测得仰角为36.9°,已知点A、B、C在同一直线上,量得AB=10米.求旗杆的高度.(结果保留一位小数,参考数据:sin25.5°≈0.43,cos25.5°≈0.90,tan25.5°≈0.48;sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75.)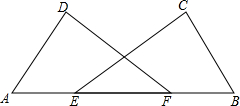 如图,已知CE=DF,∠D=∠C=90°,AE=BF,求证:AD=BC.
如图,已知CE=DF,∠D=∠C=90°,AE=BF,求证:AD=BC.