题目内容
14.已知:$\frac{4x}{{x}^{2}-4}$=$\frac{m}{x+2}$+$\frac{n}{x-2}$,求常数m,n的值.分析 根据分式的加减运算法则通分,进而得出关于m,n的等式,进而求出答案.
解答 解:∵$\frac{4x}{{x}^{2}-4}$=$\frac{m}{x+2}$+$\frac{n}{x-2}$,
∴$\frac{4x}{{x}^{2}-4}$=$\frac{m(x-2)}{(x-2)(x+2)}$+$\frac{n(x+2)}{(x-2)(x+2)}$,
则4x=(m+n)x-2(m-n),
故m+n=4,m-n=0,
解得:m=2,n=2.
点评 此题主要考查了分式的加减运算,正确得出关于m,n等式是解题关键.

练习册系列答案
相关题目
9.下列函数中,当x>0时,y随x增大而增大的是( )
| A. | y=-x | B. | y=$\frac{1}{x}$ | C. | y=3-2x | D. | y=x2 |
6.某水果店老板准备去水果批发市场批发甲、乙两种水果,该批发市场时成袋批发,每袋10千克,甲水果批发价6元/千克,最少批发20千克,在此基础上,每多批发10千克,批发价降低0.3元/千克;乙水果批发价4元/千克,最少批发30千克,在此基础上,每多批发10千克,批发价降低0.2元/千克.(例:购买甲水果30千克时,批发价为5.7元/千克),设水果店老板在最少批发的基础上,多批发甲水果x袋,多批发乙水果y袋,根据上述材料,回答以下问题:
(1)根据题意,完成下了表格:
(2)当水果店老板批发甲、乙两种水果共150千克时,甲、乙两种水果批发价相同,问此时分别批发甲、乙两种水果多少千克?
(3)老板考虑到自己只带了400元,最后决定购买甲、乙两两种水果共90千克(批发甲水果需要超过20千克,乙水果需超过30千克),请你帮助水果店老板设计批发方案.
(1)根据题意,完成下了表格:
| 甲水果 | 乙水果 | |
| 数量(千克) | 20+10x | 30+10y |
| 批发价(元/千克) | 6-0.3x | 4-0.2y |
(3)老板考虑到自己只带了400元,最后决定购买甲、乙两两种水果共90千克(批发甲水果需要超过20千克,乙水果需超过30千克),请你帮助水果店老板设计批发方案.
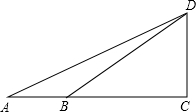 小明准备用所学数学知识测量广场上旗杆CD的高度,如图所示,在底面A处测得顶端的仰角为25.5°,在B处测得仰角为36.9°,已知点A、B、C在同一直线上,量得AB=10米.求旗杆的高度.(结果保留一位小数,参考数据:sin25.5°≈0.43,cos25.5°≈0.90,tan25.5°≈0.48;sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75.)
小明准备用所学数学知识测量广场上旗杆CD的高度,如图所示,在底面A处测得顶端的仰角为25.5°,在B处测得仰角为36.9°,已知点A、B、C在同一直线上,量得AB=10米.求旗杆的高度.(结果保留一位小数,参考数据:sin25.5°≈0.43,cos25.5°≈0.90,tan25.5°≈0.48;sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75.)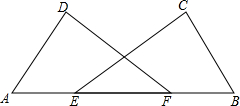 如图,已知CE=DF,∠D=∠C=90°,AE=BF,求证:AD=BC.
如图,已知CE=DF,∠D=∠C=90°,AE=BF,求证:AD=BC.