题目内容
11.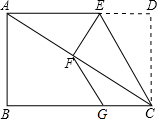 如图,已知点E是矩形一边AD上的一点,沿CE折叠矩形使点D落在对角线AC上的点F处,点G为BC上一点,且CG=DE,连FG.
如图,已知点E是矩形一边AD上的一点,沿CE折叠矩形使点D落在对角线AC上的点F处,点G为BC上一点,且CG=DE,连FG.(1)求证:FG∥EC;
(2)若∠DAC=30°,CD=4,求四边形EFGC的面积.
分析 (1)作FN∥AD交EC于N,根据翻折变换的性质证明四边形EFGC是平行四边形,根据平行四边形的性质证明即可;
(2)作FM⊥BC于M,根据直角三角形的性质和翻折变换的性质分别求出△EFC的面积和△GFC的面积即可.
解答 (1)证明:作FN∥AD交EC于N,
则FN∥BC,∠DEC=∠ENF,
由折叠的性质可知,∠DEC=∠FEN,FE=DE,
∴∠FEN=∠FNE,
∴FE=FN,又CG=DE,
∴FN=CG,又FN∥BC,
∴四边形EFGC是平行四边形,
∴FG∥EC;
(2)作FM⊥BC于M,
∵∠DAC=30°,
∴∠ACD=60°,
∴∠DCE=∠FCE=30°,又CD=4,
∴DE=$\frac{4\sqrt{3}}{3}$,
∴△EFC的面积=△EDC的面积=$\frac{1}{2}×$4×$\frac{4\sqrt{3}}{3}$=$\frac{8\sqrt{3}}{3}$,
∵∠ACB=90°-∠ACD=30°,
∴FM=$\frac{1}{2}$FC=2,
∴△FGC的面积=$\frac{1}{2}$×2×$\frac{4\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$,
∴四边形EFGC的面积=△EFC的面积+△GFC的面积=4$\sqrt{3}$.
点评 本题考查的是翻折变换和平行四边形的判定,掌握翻折变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解题的关键.

练习册系列答案
相关题目
1.下列运算正确的是( )
| A. | $\sqrt{2}+\sqrt{3}$=$\sqrt{5}$ | B. | 4x2y-x2y=4 | C. | a3•a4=a12 | D. | (a2b)3=a6b3 |
6.某水果店老板准备去水果批发市场批发甲、乙两种水果,该批发市场时成袋批发,每袋10千克,甲水果批发价6元/千克,最少批发20千克,在此基础上,每多批发10千克,批发价降低0.3元/千克;乙水果批发价4元/千克,最少批发30千克,在此基础上,每多批发10千克,批发价降低0.2元/千克.(例:购买甲水果30千克时,批发价为5.7元/千克),设水果店老板在最少批发的基础上,多批发甲水果x袋,多批发乙水果y袋,根据上述材料,回答以下问题:
(1)根据题意,完成下了表格:
(2)当水果店老板批发甲、乙两种水果共150千克时,甲、乙两种水果批发价相同,问此时分别批发甲、乙两种水果多少千克?
(3)老板考虑到自己只带了400元,最后决定购买甲、乙两两种水果共90千克(批发甲水果需要超过20千克,乙水果需超过30千克),请你帮助水果店老板设计批发方案.
(1)根据题意,完成下了表格:
| 甲水果 | 乙水果 | |
| 数量(千克) | 20+10x | 30+10y |
| 批发价(元/千克) | 6-0.3x | 4-0.2y |
(3)老板考虑到自己只带了400元,最后决定购买甲、乙两两种水果共90千克(批发甲水果需要超过20千克,乙水果需超过30千克),请你帮助水果店老板设计批发方案.
3.下列图形中既是轴对称图形又是中心对称图形的共有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
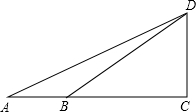 小明准备用所学数学知识测量广场上旗杆CD的高度,如图所示,在底面A处测得顶端的仰角为25.5°,在B处测得仰角为36.9°,已知点A、B、C在同一直线上,量得AB=10米.求旗杆的高度.(结果保留一位小数,参考数据:sin25.5°≈0.43,cos25.5°≈0.90,tan25.5°≈0.48;sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75.)
小明准备用所学数学知识测量广场上旗杆CD的高度,如图所示,在底面A处测得顶端的仰角为25.5°,在B处测得仰角为36.9°,已知点A、B、C在同一直线上,量得AB=10米.求旗杆的高度.(结果保留一位小数,参考数据:sin25.5°≈0.43,cos25.5°≈0.90,tan25.5°≈0.48;sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75.)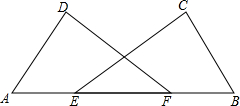 如图,已知CE=DF,∠D=∠C=90°,AE=BF,求证:AD=BC.
如图,已知CE=DF,∠D=∠C=90°,AE=BF,求证:AD=BC.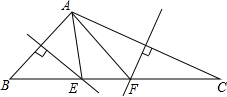 如图,在△ABC中,BC=2,∠BAC>90°,AB的垂直平分线交BC于点E,AC的垂直平分线交BC于点F.请找出图中相等的线段,并求△AEF的周长.
如图,在△ABC中,BC=2,∠BAC>90°,AB的垂直平分线交BC于点E,AC的垂直平分线交BC于点F.请找出图中相等的线段,并求△AEF的周长.