题目内容
16．
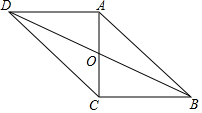如图，在?ABCD中，对角线AC、BD交于点O，AC⊥BC，且?ABCD的周长为36，△OCD的周长比△OBC的周长大2．（1）求BC，CD的长；
（2）求?ABCD的面积．
分析 （1）求出AD=BC，AB=CD，OA=OC，求出AB+BC=18，AB-BC=2，解方程组即可得出答案．
（2）利用勾股定理可求出AC的长，进而可求出?ABCD的面积．
解答 解：（1）∵四边形ABCD是平行四边形，
∴AD=BC，AB=CD，AO=OC，
∵平行四边形ABCD的周长为18，
∴DC+BC=18①，
∵△OCD的周长比△OBC的周长大22，
∴（AB+AO+OB）-（BC+OB+OC）=2，
∴CD-BC=2②，
①+②得：2CD=20，
CD=10，
①-②得：2BC=16，
BC=8；
（2）∵BC=8，AB=CD=10，AC⊥BC，
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=6，
∴?ABCD的面积=6×8=48．
点评 本题考查了平行四边形性质的应用以及勾股定理和平行四边形的面积公式运用，熟记平行四边形的各种性质是解题的关键．
练习册系列答案
相关题目
如图，将边长为4的正方形ABCD沿其对角线AC剪开，固定△ADC，并把△ABC沿着AD方向平移，得到△A′B′C′，当两个三角形重叠部分的面积为2时，它移动的距离AA′等于2+$\sqrt{2}$或2-$\sqrt{2}$．
如图，在平面直角坐标系中，点A的坐标为（3，0），B为直线y=$\frac{\sqrt{3}}{3}$x上的一个动点，延长AB至C，使得AB=BC，过点C作CD⊥x轴于点D，交直线OB于点F，过点A作AE∥OB，交直线CD于点E．
11．矩形有而平行四边形没有的性质是（ ）
| A． | 对角相等 | B． | 对边相等 | C． | 邻角互补 | D． | 对角线相等 |
