题目内容
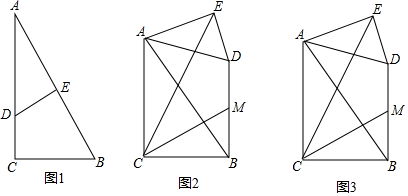
5.如图1,在Rt△ABC中,D是边AC上一点(不与端点A,C重合),过点D作DE⊥AB于点E,将△ADE绕点A以每秒30°的速度逆时针方向旋转,运动时间为t(0≤t≤12)秒,取BD的中点M,连接CM,CE.(1)如图2,若∠ABC=60°,当∠MCE=$\frac{1}{2}$∠CAD,0≤t≤6时,直接写出t的值为2s;
(2)如图3,若∠ABC=α,用含α的式子表示∠MCE的度数,并说明理由;
(3)若∠ABC=60°,AD=2,AC=3,当线段AD绕点A逆时针方向旋转一周的过程中,写出线段CM长度的最大值和最小值,并指出相应t的值(不要求证明).
分析 (1)如图1中,延长CM到H,使得MH=CM,连接DH,EH.首先证明△EAC∽△EDH,推出∠ECH=30°,∠DAC=30°,由此即可解决问题;
(2)结论:∠ECM=90°-α,如图2中,延长CM到H,使得MH=CM,连接DH,EH.证明方法类似(1);
(3)如图3中,取AB的中点H,连接CH、HM.易知CH=$\sqrt{3}$,HM=1,在△HCM中,利用三边关系即可解决问题;
解答 解:(1)如图1中,延长CM到H,使得MH=CM,连接DH,EH.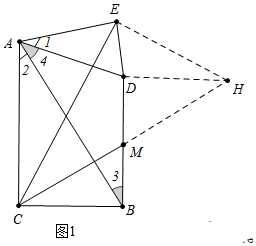
∵∠ABC=∠ADE=60°,∠ACB=∠AED=90°
∴∠1=∠2=30°,
∴∠EAC=60°+∠4,
∵DM=BM∠DMH=∠CMB,MH=MC,
∴△DMH≌△BMC,
∴∠HDM=∠CBM,DH=BC,
∴∠EDH=360°-60°-∠ADB-∠HDM=300°-(180°-∠4-∠3)-∠3-60°=60°+∠4,
∴∠EAC=∠EDH,
∵$\frac{AE}{DE}$=$\frac{AC}{BC}$=$\sqrt{3}$,
∴$\frac{AE}{DE}$=$\frac{AC}{DH}$,
∴△EAC∽△EDH,
∴$\frac{EC}{EH}$=$\frac{EA}{ED}$=$\sqrt{3}$,∠AEC=∠DEH,
∴∠CEH=∠AED=90°,
∴tan∠ECH=$\frac{EH}{EC}$=$\frac{\sqrt{3}}{3}$,
∴∠ECH=30°,
∵∠ECH=$\frac{1}{2}$∠DAC,
∴∠DAB=30°,
∴AD∥BC,
∴∠DAC=90°,
∴t=$\frac{60}{30}$=2s.
故答案为2s.
(2)结论:∠ECM=90°-α,
理由:如图2中,延长CM到H,使得MH=CM,连接DH,EH.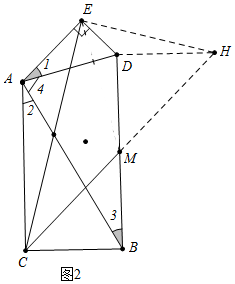
∵∠ABC=∠ADE,∠ACB=∠AED=90°
∴∠1=∠2,
∴∠EAC=2∠1+∠4,
∵DM=BM∠DMH=∠CMB,MH=MC,
∴△DMH≌△BMC,
∴∠HDM=∠CBM,DH=BC,
∴∠EDH=360°-∠ADE-∠ADB-∠HDM=360°-(90°-∠1)-(180°-∠4-∠3)-∠3-(90°-∠1)=2∠1+∠4,
∴∠EAC=∠EDH,
∵$\frac{AE}{DE}$=$\frac{AC}{BC}$=tanα,
∴$\frac{AE}{DE}$=$\frac{AC}{DH}$,
∴△EAC∽△EDH,
∴$\frac{EC}{EH}$=$\frac{EA}{ED}$=tanα,∠AEC=∠DEH,
∴∠CEH=∠AED=90°,
∴tan∠EHC=$\frac{EC}{EH}$=tanα,
∴∠EHC=α,
∴∠ECM=90°-α,
(3)如图3中,取AB的中点H,连接CH、HM.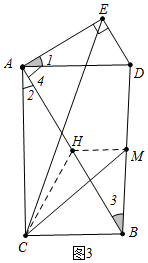
在Rt△ABC中,∵AC=3,∠ABC=60°,
∴sin60°=$\frac{AC}{AB}$,
∴AB=2$\sqrt{3}$,
∵AH=HB,
∴CH=$\frac{1}{2}$AB=$\sqrt{3}$,
∵AH=HB,DM=MB,
∴HM=$\frac{1}{2}$AD=1,
∵CH+HM≥CM≥CH-HM,
∴1+$\sqrt{3}$≥CM≥$\sqrt{3}$-1,
∴CM的最大值为1+$\sqrt{3}$.CM的最小值为$\sqrt{3}$-1.
当CM最大时,t=$\frac{150}{30}$=5s,
当CM的值最小时,t=$\frac{330}{30}$=11s.
点评 本题考查几何变换综合题、相似三角形的判定和性质、锐角三角函数、三角形三边关系、直角三角形斜边中线定理等知识,解题的关键是学会添加常用辅助线,构造相似三角形或全等三角形解决问题,属于中考压轴题.

 某体育用品商场为了推销一种品牌运动服,先做了市场调查,得到数据如下表:
某体育用品商场为了推销一种品牌运动服,先做了市场调查,得到数据如下表:| 卖出价格x(元/件) | 50 | 51 | 52 | 53 |
| 销售量p(件) | 500 | 490 | 480 | 470 |
(2)如果这种运动服的买入价为每件40元,试求销售利润y(元)与卖出价格x(元/件)的函数关系式(销售利润=销售收入-买入支出);
(3)在(2)的条件下,当卖出价为多少时,能获得最大利润?最大利润为多少?
| A. | $\frac{1}{6}$ | B. | 8 | C. | $\frac{1}{8}$ | D. | $\frac{3}{2}$ |
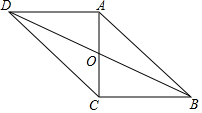 如图,在?ABCD中,对角线AC、BD交于点O,AC⊥BC,且?ABCD的周长为36,△OCD的周长比△OBC的周长大2.
如图,在?ABCD中,对角线AC、BD交于点O,AC⊥BC,且?ABCD的周长为36,△OCD的周长比△OBC的周长大2.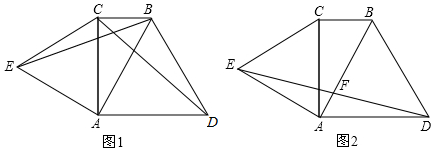
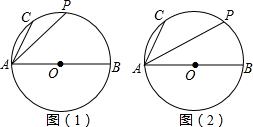 如图,AB是⊙O的直径,C、P是弧AB上两点,AB=25,AC=7.
如图,AB是⊙O的直径,C、P是弧AB上两点,AB=25,AC=7.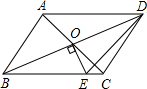 如图,已知?ABCD的对角线交于点O,且AD≠CD,过O作OE⊥BD交BC于E点,若△CDE的周长是8,则?ABCD的周长为16.
如图,已知?ABCD的对角线交于点O,且AD≠CD,过O作OE⊥BD交BC于E点,若△CDE的周长是8,则?ABCD的周长为16. (1)在同一平面直角坐标系中描出下列各点,并将各点用线段依次连接起来:
(1)在同一平面直角坐标系中描出下列各点,并将各点用线段依次连接起来: