题目内容
17.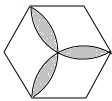 向如图所示的正六边形靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为( )
向如图所示的正六边形靶子上随意抛一枚飞镖,则飞镖插在阴影区域的概率为( )| A. | $\frac{2\sqrt{3}-π}{π}$ | B. | $\frac{2π\sqrt{3}-9}{9}$ | C. | $\frac{π-\sqrt{3}}{π}$ | D. | $\frac{π\sqrt{3}-4}{9}$ |
分析 根据已知假设出六边形边长为1,进而求出正六边形面积和S扇形FAB,S扇形BCD,S扇形DEF,再利用三个扇形面积减去正六边形面积等于阴影部分面积,进而得出飞镖插在阴影区域的概率.
解答 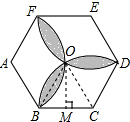 解:根据图象可以知,O为正六边形中心,过点O作OM⊥BC,
解:根据图象可以知,O为正六边形中心,过点O作OM⊥BC,
设正六边形边长为1,根据正六边形每个内角为120°,
则S扇形FAB=$\frac{120π×{1}^{2}}{360}$=$\frac{π}{3}$,
∴S扇形BCD=$\frac{120π×{1}^{2}}{360}$=$\frac{π}{3}$,S扇形DEF=$\frac{120π×{1}^{2}}{360}$=$\frac{π}{3}$,
∵OC=BC=BO=1,OM⊥BC,
∴OM=$\sqrt{{1}^{2}-(\frac{1}{2})^{2}}$=$\frac{\sqrt{3}}{2}$,
∴S△OBC=$\frac{1}{2}$×OM×BC=$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$×1=$\frac{\sqrt{3}}{4}$,
∴S正六边形面积=$\frac{\sqrt{3}}{4}$×6=$\frac{3\sqrt{3}}{2}$,
∴S阴影=π-$\frac{3-\sqrt{3}}{2}$,
∴飞镖插在阴影区域的概率为:$\frac{π-\frac{3\sqrt{3}}{2}}{\frac{3\sqrt{3}}{2}}$=$\frac{2\sqrt{3}π}{9}$-1=$\frac{2\sqrt{3}π-9}{9}$;
故选B.
点评 此题主要考查了概率公式以及正六边形面积求法和扇形面积公式等知识,根据已知得出三个扇形面积减去正六边形面积等于阴影部分面积是解题关键.

练习册系列答案
相关题目
8.下列运算正确的是( )
| A. | 6a-5a=1 | B. | (a2)3=a5 | C. | (-2x2y)3=-6x6y3 | D. | 3ab2•(-a)=-3a2b2 |
12. 如图,AB∥CD,EF⊥AB于E,EF交CD于F,已知∠1=50°,则∠2=( )
如图,AB∥CD,EF⊥AB于E,EF交CD于F,已知∠1=50°,则∠2=( )
 如图,AB∥CD,EF⊥AB于E,EF交CD于F,已知∠1=50°,则∠2=( )
如图,AB∥CD,EF⊥AB于E,EF交CD于F,已知∠1=50°,则∠2=( )| A. | 40° | B. | 50° | C. | 60° | D. | 130° |
2.将图1的正四角锥ABCDE沿着其中的四个边剪开后,形成的展开图为图2.判断下列哪一个选项中的四个边可为此四个边?( )
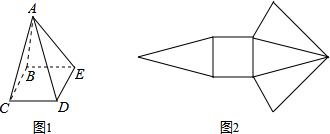

| A. | AC、AD、BC、DE | B. | AB、BE、DE、CD | C. | AC、BC、AE、DE | D. | AC、AD、AE、BC |
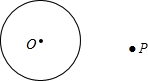 我们在探索“圆”时,学习了圆周角与圆心角的关系定理的推论“直径所对的圆周角是直角”.请利用此推论,完成下面的尺规作图.如图,点P是⊙O外的一点,用圆规和直尺过点P作出⊙O的切线.(要求:不写作法,保留作图痕迹,写出结论)
我们在探索“圆”时,学习了圆周角与圆心角的关系定理的推论“直径所对的圆周角是直角”.请利用此推论,完成下面的尺规作图.如图,点P是⊙O外的一点,用圆规和直尺过点P作出⊙O的切线.(要求:不写作法,保留作图痕迹,写出结论)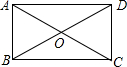 如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AB=1,则BC的长为$\sqrt{3}$.
如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AB=1,则BC的长为$\sqrt{3}$.