题目内容
19. 如图,点E在正方形ABCD的边AD上,已知AE=7,CE=13,则阴影部分的面积是( )
如图,点E在正方形ABCD的边AD上,已知AE=7,CE=13,则阴影部分的面积是( )| A. | 114 | B. | 124 | C. | 134 | D. | 144 |
分析 由正方形的性质得出∠D=90°,AB=BC=AD,设AB=BC=AD=x,则DE=x-7,根据勾股定理得出CD2+DE2=CE2,得出方程x2+(x-7)2=132,解方程求出BC=AB=12,即可得出阴影部分的面积=$\frac{1}{2}$(AE+BC)•AB.
解答 解:∵四边形ABCD是正方形,
∴∠D=90°,AB=BC=AD,
设AB=BC=AD=x,
则DE=x-7,
∵CD2+DE2=CE2,
∴x2+(x-7)2=132,
解得:x=12,或x=-5(不合题意,舍去),
∴BC=AB=12,
∴阴影部分的面积=$\frac{1}{2}$(AE+BC)•AB=$\frac{1}{2}$×(7+12)×12=114;
故选:A.
点评 本题考查了正方形的性质、勾股定理、以及梯形面积的计算;熟练掌握正方形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
11. 如图所示,AB∥CD,∠D=26°,∠E=35°,则∠ABE的度数是( )
如图所示,AB∥CD,∠D=26°,∠E=35°,则∠ABE的度数是( )
 如图所示,AB∥CD,∠D=26°,∠E=35°,则∠ABE的度数是( )
如图所示,AB∥CD,∠D=26°,∠E=35°,则∠ABE的度数是( )| A. | 61° | B. | 71° | C. | 109° | D. | 119° |
8.从标号分别为1,2,3,4,5的5张卡片中,随机抽取1张,下列事件中,必然事件是( )
| A. | 该卡片标号小于6 | B. | 该卡片标号大于6 | ||
| C. | 该卡片标号是奇数 | D. | 该卡片标号是3 |
9.下列说法正确的是( )
| A. | 过一点有且只有一条直线与已知直线平行 | |
| B. | 三角形的三条高线都在三角形的内部 | |
| C. | 两条直线被第三条直线所截,同旁内角互补 | |
| D. | 平移前后图形的形状和大小都没有发生改变 |
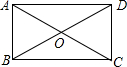 如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AB=1,则BC的长为$\sqrt{3}$.
如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AB=1,则BC的长为$\sqrt{3}$. 如图,面积为8cm2的正方形OABC的边OA,OC在坐标轴上,点P从点O出发,以每秒1个单位长度的速度沿x轴向点C运动;同时点Q从C点出发以相同的速度沿x轴的正方向运动,规定P点到达点C时,点Q也停止运动,过点Q作平行于y轴的直线l.连结AP,过P作AP的垂线交l于点D,连结AD,AD交BC于点E.设点P运动的时间为t秒.
如图,面积为8cm2的正方形OABC的边OA,OC在坐标轴上,点P从点O出发,以每秒1个单位长度的速度沿x轴向点C运动;同时点Q从C点出发以相同的速度沿x轴的正方向运动,规定P点到达点C时,点Q也停止运动,过点Q作平行于y轴的直线l.连结AP,过P作AP的垂线交l于点D,连结AD,AD交BC于点E.设点P运动的时间为t秒.