题目内容
4.看图回答问题:
(1)内角和为2014°,小明为什么不说不可能?
(2)小华求的是几边形的内角和?
(3)错把外角当内角的那个外角的度数你能求出来吗?它是多少度?
分析 (1)n边形的内角和是(n-2)•180°,因而内角和一定是180度的倍数,依此即可作出判断;
(2)多边形的内角一定大于0,并且小于180度,因而内角和再加上一个内角的值,这个值除以180度,所得数值比边数n-2要大,大的值小于1.则用2014除以180所得值,加上2,比这个数小的最大的整数就是多边形的边数;
(3)用2014°-1980°即可.
解答 解:(1)∵n边形的内角和是(n-2)•180°,
∴内角和一定是180度的倍数,
∵2014÷180=11…34,
∴内角和为2014°不可能;
(2)依题意有(x-2)•180°<2014°,
解得x<13$\frac{17}{90}$.
因而多边形的边数是13,
故小华求的是十三边形的内角和;
(3)13边形的内角和是(13-2)×180°=1980°,
2014°-1980°=34°,
因此这个外角的度数为34°.
点评 考查了多边形的内角与外角,解决本题的关键是正确运用多边形的内角和公式,是需要熟记的内容.

练习册系列答案
相关题目
14. 已知如图:点A、B、C、D在⊙O上,AB为直径,∠ABC=72°,则∠D为( )
已知如图:点A、B、C、D在⊙O上,AB为直径,∠ABC=72°,则∠D为( )
 已知如图:点A、B、C、D在⊙O上,AB为直径,∠ABC=72°,则∠D为( )
已知如图:点A、B、C、D在⊙O上,AB为直径,∠ABC=72°,则∠D为( )| A. | 18° | B. | 30° | C. | 36° | D. | 72° |
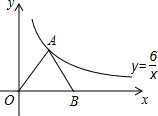 如图,点A在双曲线y=$\frac{6}{x}$上,B为x轴正半轴上一点,连结OA、AB且AO=AB,则△AOB的面积是6.
如图,点A在双曲线y=$\frac{6}{x}$上,B为x轴正半轴上一点,连结OA、AB且AO=AB,则△AOB的面积是6.