题目内容
13.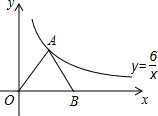 如图,点A在双曲线y=$\frac{6}{x}$上,B为x轴正半轴上一点,连结OA、AB且AO=AB,则△AOB的面积是6.
如图,点A在双曲线y=$\frac{6}{x}$上,B为x轴正半轴上一点,连结OA、AB且AO=AB,则△AOB的面积是6.
分析 作AC⊥x轴于C,如图,根据等腰三角形的性质得OC=BC,则利用三角形面积公式得到S△AOC=S△ABC,再利用反比例函数的比例系数k的几何意义得S△AOC=$\frac{1}{2}$•|6|=3,所以S△AOB=2S△AOC=6.
解答  解:作AC⊥x轴于C,如图,
解:作AC⊥x轴于C,如图,
∵AO=AB,
∴OC=BC,
∴S△AOC=S△ABC,
而S△AOC=$\frac{1}{2}$•|6|=3,
∴S△AOB=2S△AOC=6.
故答案为6.
点评 本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=kx图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.

练习册系列答案
相关题目
18.某里弄所有的263户家庭人口数分组表示如下:
计算总体均值μ,中位数m,方差s2和标准差s.
| 家庭人口数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 家庭数 | 20 | 29 | 48 | 50 | 46 | 36 | 19 | 8 | 4 | 3 |
5.已知三角形的两边长分别为5cm和11cm,则下列长度的四条线段中能作为第三边的是( )
| A. | 16cm | B. | 9cm | C. | 6cm | D. | 5cm |