Question

19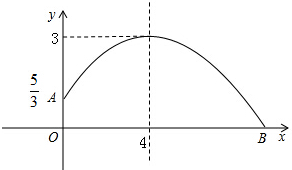．小亮推铅球时，铅球行进高度y（m）与水平距离x（m）之间的关系如图所示（二次函数图象的一部分）．
（1）求y与x之间的函数关系式；
（2）求小亮推出铅球的水平距离．

Answer 1

分析 （1）由图象可知该函数为二次函数，顶点为（4，3），过点（0，$\frac{5}{3}$），因此设抛物线的顶点式，从而可以求得y与x之间的函数关系式；
（2）令第一问中函数解析式中的y=0，可以求得相应的x的值，根据实际情况，推出的水平距离为正值，从而可以解答本题．

解答 解：（1）设y与x之间的函数关系式为：y=a（x-4）²+3，
∵点（0，$\frac{5}{3}$）在y=a（x-4）²+3的图象上，
∴$\frac{5}{3}=a（0-4）^{2}+3$
解得，a=$-\frac{1}{12}$，
∴y与x之间的函数关系式是：y=$-\frac{1}{12}{（x-4）}^{2}+3$；
（2）将y=0代入y=$-\frac{1}{12}{（x-4）}^{2}+3$，得
0=$-\frac{1}{12}{（x-4）}^{2}+3$，
解得x₁=-2，x₂=10
由图可知，小亮推出的距离为正值，故小亮推出铅球的水平距离是10m，
即小亮推出铅球的水平距离是10m．

点评 本题考查二次函数的应用，解题的关键是明确题意，列出相应的函数关系式，并且可以求得抛物线与x轴的交点．