题目内容
14.计算:先化简,再求值:($\frac{2}{x+3}$-$\frac{1}{3-x}$)÷$\frac{x}{{x}^{2}-9}$,其中x=1.分析 先算括号里面的,再算除法,最后把x的值代入进行计算即可.
解答 解:原式=$\frac{2(x-3)+(x+3)}{(x+3)(x-3)}$÷$\frac{x}{{x}^{2}-9}$
=$\frac{3(x-1)}{(x+3)(x-3)}$•$\frac{(x+3)(x-3)}{x}$
=$\frac{3(x-1)}{x}$,
当x=1时,原式=0.
点评 本题考查的是分式的化简求值,此类题型的特点是:利用方程解的定义找到相等关系,再把所求的代数式化简后整理出所找到的相等关系的形式,再把此相等关系整体代入所求代数式,即可求出代数式的值.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
4.下列命题是假命题的是( )
| A. | 若a2=b2,则a=b | |
| B. | 两直线平行,同位角相等 | |
| C. | 对顶角相等 | |
| D. | 若b2-4ac>0,则方程ax2+bx+c=0(a≠0)有两个不等的实数根 |
19.下列事件中,属于不可能事件的是( )
| A. | 射击运动员射击一次,命中9环 | |
| B. | 今天是星期六,明天就是星期一 | |
| C. | 某种彩票中奖率为10%,买十张有一张中奖 | |
| D. | 在只装有10个红球的布袋中摸出一球,这个球一定是红球 |
13.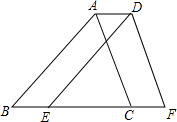 如图,将三角形ABC沿BC方向平移到三角形DEF,若AD=1,CE=3,则梯形ABFD的面积与三角形ABC的面积比是( )
如图,将三角形ABC沿BC方向平移到三角形DEF,若AD=1,CE=3,则梯形ABFD的面积与三角形ABC的面积比是( )
 如图,将三角形ABC沿BC方向平移到三角形DEF,若AD=1,CE=3,则梯形ABFD的面积与三角形ABC的面积比是( )
如图,将三角形ABC沿BC方向平移到三角形DEF,若AD=1,CE=3,则梯形ABFD的面积与三角形ABC的面积比是( )| A. | 2:1 | B. | 3:2 | C. | 4:3 | D. | 不能确定 |

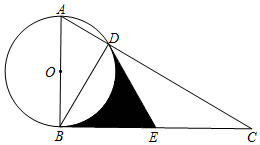 如图,Rt△ABC中,∠ABC为直角,以AB为直径作⊙O交AC于点D,点E为BC中点,连结DE,DB
如图,Rt△ABC中,∠ABC为直角,以AB为直径作⊙O交AC于点D,点E为BC中点,连结DE,DB