题目内容
2.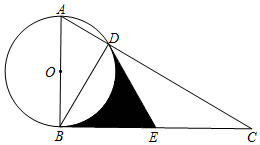 如图,Rt△ABC中,∠ABC为直角,以AB为直径作⊙O交AC于点D,点E为BC中点,连结DE,DB
如图,Rt△ABC中,∠ABC为直角,以AB为直径作⊙O交AC于点D,点E为BC中点,连结DE,DB(1)求证:DE与⊙O相切;
(2)若∠C=30°,求∠BOD的度数;
(3)在(2)的条件下,若⊙O半径为2,求阴影部分面积.
分析 (1)欲证明DE与⊙O相切,只要证明∠ODE=90°即可.
(2)在四边形OBED中,利用四边形内角和求∠BOD即可.
(3)根据S阴影部分=S四边形OBED-S扇形OBD=S△OBE+S△ODE-S扇形OBD计算即可.
解答 解:(1)连结OD,
∵AB为⊙O为直径,
∴∠ADB=∠BDC=90°,
又∵E是斜边BC的中点
∴DE=BE=CE,
∴∠BDE=∠DBE,
∵OD=OB,
∴∠ODB=∠OBD
∴∠ODE=∠ODB+∠BDE=∠OBD+∠DBE=∠ABC=90°
即DE与⊙O相切.
(也可以通过证明△OBE≌△ODE得到∠ODE=∠OBE=90°)
(2)若∠C=30°而DE=CE,
∴∠DEB=60°
在四边形OBED中,则∠BOD=360°-90°-90°-60°=120°,
(3)连结OE,则∠OED=∠OEB=30°
∵OD=OB=2∴DE=BE=2$\sqrt{3}$
∴S阴影部分=S四边形OBED-S扇形OBD=S△OBE+S△ODE-S扇形OBD
=2$\sqrt{3}$+2$\sqrt{3}$-$\frac{120π×22}{360}$=4$\sqrt{3}$-$\frac{4π}{3}$.
点评 本题考查切线的判定、扇形的面积公式、四边形的内角和等知识,解题的关键是学会添加常用辅助线,学会用分割法求阴影部分面积,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.下列各式中,正确的是( )
| A. | $\root{3}{-5}$=-$\root{3}{5}$ | B. | $\sqrt{16}$=±4 | C. | $\sqrt{(-13)^{2}}$=-13 | D. | $\sqrt{3.6}$=0.6 |
10.下列计算正确的是( )
| A. | x+x2=x3 | B. | 2x-3x=-x | C. | (x2)3=x5 | D. | x6÷x3=x2 |
 如图,菱形ABCD边长为9,DF交AC于点E,且AE=AF=6,则EF的长为2$\sqrt{3}$.
如图,菱形ABCD边长为9,DF交AC于点E,且AE=AF=6,则EF的长为2$\sqrt{3}$.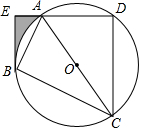 如图,四边形ABCD内接于⊙O,AC是⊙O的直径,过点B作BE⊥AD,垂足为点E,AB平分∠CAE.
如图,四边形ABCD内接于⊙O,AC是⊙O的直径,过点B作BE⊥AD,垂足为点E,AB平分∠CAE.