题目内容
16.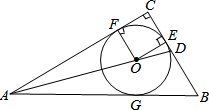 如图,⊙O是Rt△ABC的内切圆,∠C=90°,AO的延长线交BC于点D,若AC=6,CD=2,则⊙O的半径$\frac{3}{2}$.
如图,⊙O是Rt△ABC的内切圆,∠C=90°,AO的延长线交BC于点D,若AC=6,CD=2,则⊙O的半径$\frac{3}{2}$.
分析 首先证明四边形CEOF是正方形.设圆O的半径为r,则DE=2-r,OE=r,然后证明△OED∽△ACD,最后依据相似三角形的性质列方程求解即可.
解答 解:∵⊙O是Rt△ABC的内切圆,
∴OF=OE,OF⊥AC,OE⊥BC,
又∵∠C=90°,
∴CEOF是正方形.
设圆O的半径为r,则DE=2-r,OE=r.
∵CEOF是正方形,
∴OE∥AC.
∴△OED∽△ACD.
∴$\frac{OE}{AC}=\frac{ED}{CD}$即$\frac{r}{6}=\frac{2-r}{2}$.
解得:r=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题主要考查的是三角形的内心的性质、相似三角形的性质和判定、正方形的判定、切线的性质,依据相似三角形的性质列出关于r的方程是解题的关键.

练习册系列答案
相关题目
4. 如图,BC是⊙O的直径,AC是⊙O的切线,连接AB交⊙O于点D,连接OD,已知AD=2,∠A=2∠B,则扇形BOD的面积是( )
如图,BC是⊙O的直径,AC是⊙O的切线,连接AB交⊙O于点D,连接OD,已知AD=2,∠A=2∠B,则扇形BOD的面积是( )
 如图,BC是⊙O的直径,AC是⊙O的切线,连接AB交⊙O于点D,连接OD,已知AD=2,∠A=2∠B,则扇形BOD的面积是( )
如图,BC是⊙O的直径,AC是⊙O的切线,连接AB交⊙O于点D,连接OD,已知AD=2,∠A=2∠B,则扇形BOD的面积是( )| A. | 2π | B. | 4π | C. | $\sqrt{3}$π | D. | 2$\sqrt{3}$π |
11.在实数$\sqrt{8}$,2π,$\root{3}{-27}$,sin45°中,是有理数的是( )
| A. | $\sqrt{8}$ | B. | 2π | C. | $\root{3}{-27}$ | D. | sin45° |
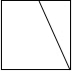
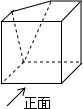 如图是正方形切去一个角后形成的几何体,则该几何体的左视图为( )
如图是正方形切去一个角后形成的几何体,则该几何体的左视图为( )

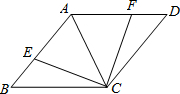 如图,AC是菱形ABCD的对角线,点E、F分别在边AB、AD上,且AE=AF.
如图,AC是菱形ABCD的对角线,点E、F分别在边AB、AD上,且AE=AF.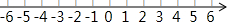 解下列不等式组,并将它的解集在数轴上表示出来.
解下列不等式组,并将它的解集在数轴上表示出来.