题目内容
6.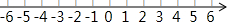 解下列不等式组,并将它的解集在数轴上表示出来.
解下列不等式组,并将它的解集在数轴上表示出来.$\left\{\begin{array}{l}{x-1>2x}\\{\frac{x-1}{3}≤\frac{x+1}{9}}\end{array}\right.$.
分析 先分别求出各不等式的解集,再求出其公共解集并在数轴上表示出来即可.
解答 解:
$\left\{\begin{array}{l}{x-1>2x①}\\{\frac{x-1}{3}≤\frac{x+1}{9}②}\end{array}\right.$
由①得,x<-1,
由②得,x≤2,
故此不等式组的解集为:x<-1
在数轴上表示为:
点评 本题考查的是在数轴上表示一元一次不等式组的解集及解一元一次不等式组,熟知实心圆点与空心圆点的区别是解答此题的关键

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
14.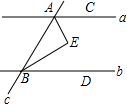 如图,a,b为平面内两条直线,且a∥b,直线c截a,b于A,B两点,C,D分别为a,b上的点,在平面内有一点E,EA,EB分别平分∠BAC和∠ABD,则∠E等于( )
如图,a,b为平面内两条直线,且a∥b,直线c截a,b于A,B两点,C,D分别为a,b上的点,在平面内有一点E,EA,EB分别平分∠BAC和∠ABD,则∠E等于( )
 如图,a,b为平面内两条直线,且a∥b,直线c截a,b于A,B两点,C,D分别为a,b上的点,在平面内有一点E,EA,EB分别平分∠BAC和∠ABD,则∠E等于( )
如图,a,b为平面内两条直线,且a∥b,直线c截a,b于A,B两点,C,D分别为a,b上的点,在平面内有一点E,EA,EB分别平分∠BAC和∠ABD,则∠E等于( )| A. | 90° | B. | 80° | C. | 60° | D. | 100° |
11.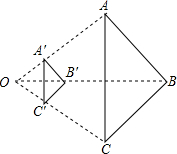 如图,以点O为位似中心,将△ABC缩小后得到△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为( )
如图,以点O为位似中心,将△ABC缩小后得到△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为( )
 如图,以点O为位似中心,将△ABC缩小后得到△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为( )
如图,以点O为位似中心,将△ABC缩小后得到△A′B′C′,已知OB=3OB′,则△A′B′C′与△ABC的面积比为( )| A. | 1:3 | B. | 1:4 | C. | 1:5 | D. | 1:9 |
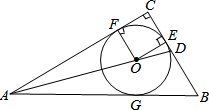 如图,⊙O是Rt△ABC的内切圆,∠C=90°,AO的延长线交BC于点D,若AC=6,CD=2,则⊙O的半径$\frac{3}{2}$.
如图,⊙O是Rt△ABC的内切圆,∠C=90°,AO的延长线交BC于点D,若AC=6,CD=2,则⊙O的半径$\frac{3}{2}$. 如图,已知在△ABC中,点D在边AC上,CD:AD=1:2,$\overrightarrow{BA}=\overrightarrow a$,$\overrightarrow{BC}=\overrightarrow b$,
如图,已知在△ABC中,点D在边AC上,CD:AD=1:2,$\overrightarrow{BA}=\overrightarrow a$,$\overrightarrow{BC}=\overrightarrow b$,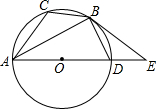 如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,且BD=BC,延长AD到E,且有∠EBD=∠CAB.
如图,已知⊙O是△ABC的外接圆,AD是⊙O的直径,且BD=BC,延长AD到E,且有∠EBD=∠CAB.