题目内容
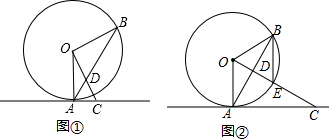
4. 如图,BC是⊙O的直径,AC是⊙O的切线,连接AB交⊙O于点D,连接OD,已知AD=2,∠A=2∠B,则扇形BOD的面积是( )
如图,BC是⊙O的直径,AC是⊙O的切线,连接AB交⊙O于点D,连接OD,已知AD=2,∠A=2∠B,则扇形BOD的面积是( )| A. | 2π | B. | 4π | C. | $\sqrt{3}$π | D. | 2$\sqrt{3}$π |
分析 连结CD,如图,先利用圆周角定理和切线的性质得到∠BDC=90°,BC⊥AC,则利用∠A=2∠B可计算出∠B=30°,再判断△ODC为等边三角形得到OD=CD,∠OCD=60°,接着在Rt△ADC中利用含30度的直角三角形三边的关系求出CD=$\sqrt{3}$AD=2$\sqrt{3}$,则OD=2$\sqrt{3}$,然后根据扇形面积公式计算扇形BOD的面积.
解答 解:连结CD,如图,
∵BC是⊙O的直径,AC是⊙O的切线,
∴∠BDC=90°,BC⊥AC,
∴∠ACB=90°,
∴∠A+∠B=90°,
而∠A=2∠B,
∴2∠B+∠B=90°,即得∠B=30°,
∴∠DOC=2∠B=60°,
∴△ODC为等边三角形,
∴OD=CD,∠OCD=60°,
∴∠ACD=30°,
在Rt△ADC中,CD=$\sqrt{3}$AD=2$\sqrt{3}$,
∴OD=2$\sqrt{3}$
而∠BOD=180°-∠DOC=120°,
∴扇形BOD的面积=$\frac{120•π•(2\sqrt{3})^{2}}{360}$=4π.
故选B.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了圆周角定理和扇形的面积公式.

练习册系列答案
相关题目
14.2015年10月18日,TCL2015长沙国际马拉松赛正式开赛,来自国内外的1.5万余名选手在长沙这座美丽的城市中奔跑.马拉松长跑是国际上非常普及的长跑比赛项目,全程距离约为42千米,将数据42千米用科学记数法表示为( )
| A. | 42×103米 | B. | 0.42×105米 | C. | 4.2×104米 | D. | 4.2×105米 |
15.下列各式计算正确的是( )
| A. | $\sqrt{2}$•$\sqrt{3}$=$\sqrt{5}$ | B. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ | C. | x3•x5=x15 | D. | x11÷x6=x5 |
9.下列各运算中,正确的是( )
| A. | 30+3-3=-3 | B. | $\sqrt{5}-\sqrt{2}$=$\sqrt{3}$ | C. | (2a2)3=6a6 | D. | -a8÷a4=-a4 |
 已知下列命题为真命题的是①②④(只填序号).
已知下列命题为真命题的是①②④(只填序号).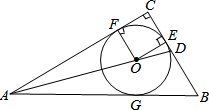 如图,⊙O是Rt△ABC的内切圆,∠C=90°,AO的延长线交BC于点D,若AC=6,CD=2,则⊙O的半径$\frac{3}{2}$.
如图,⊙O是Rt△ABC的内切圆,∠C=90°,AO的延长线交BC于点D,若AC=6,CD=2,则⊙O的半径$\frac{3}{2}$.
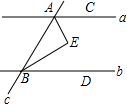 如图,a,b为平面内两条直线,且a∥b,直线c截a,b于A,B两点,C,D分别为a,b上的点,在平面内有一点E,EA,EB分别平分∠BAC和∠ABD,则∠E等于( )
如图,a,b为平面内两条直线,且a∥b,直线c截a,b于A,B两点,C,D分别为a,b上的点,在平面内有一点E,EA,EB分别平分∠BAC和∠ABD,则∠E等于( )