题目内容
5．
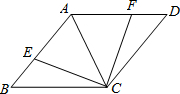如图，AC是菱形ABCD的对角线，点E、F分别在边AB、AD上，且AE=AF．求证：△BCE≌△DCF．
分析 直接利用菱形的性质得出BC=DC=AB=AD，∠B=∠D，进而结合全等三角形的判定方法得出答案．
解答 证明：∵四边形ABCD是菱形，
∴BC=DC=AB=AD，∠B=∠D，
∵AE=AF，
∴BE=DF，
在△BCE和△DCF中
∵$\left\{\begin{array}{l}{BC=DC}\\{∠B=∠D}\\{BE=DF}\end{array}\right.$，
∴△BCE≌△DCF（SAS）．
点评 此题主要考查了菱形的性质以及全等三角形的判定，正确掌握菱形的性质是解题关键．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
15．下列各式计算正确的是（ ）
| A． | $\sqrt{2}$•$\sqrt{3}$=$\sqrt{5}$ | B． | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ | C． | x3•x5=x15 | D． | x11÷x6=x5 |
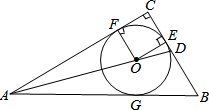如图，⊙O是Rt△ABC的内切圆，∠C=90°，AO的延长线交BC于点D，若AC=6，CD=2，则⊙O的半径$\frac{3}{2}$．
20．
如图，D为等边三角形ABC内的一点，DA=5，DB=4，DC=3，将线段AD以点A为旋转中心逆时针旋转60°，得到线段AD′，连接DD′，则tan∠DD′C=（ ）
如图，D为等边三角形ABC内的一点，DA=5，DB=4，DC=3，将线段AD以点A为旋转中心逆时针旋转60°，得到线段AD′，连接DD′，则tan∠DD′C=（ ）| A． | $\frac{4}{3}$ | B． | $\frac{3}{4}$ | C． | $\frac{5}{4}$ | D． | $\frac{4}{5}$ |
如图，已知在△ABC中，点D在边AC上，CD：AD=1：2，$\overrightarrow{BA}=\overrightarrow a$，$\overrightarrow{BC}=\overrightarrow b$，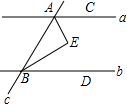
如图，a，b为平面内两条直线，且a∥b，直线c截a，b于A，B两点，C，D分别为a，b上的点，在平面内有一点E，EA，EB分别平分∠BAC和∠ABD，则∠E等于（ ）