题目内容
8.菱形ABCD的周长为20cm,两条对角线AC:BD=4:3,那么对角线AC长( )| A. | 5cm | B. | 6cm | C. | 8cm | D. | 10cm |
分析 根据菱形的性质求出AD,AO=OC,BO=DO,AC⊥BD,设AO=4xcm,DO=3xcm,根据勾股定理得出方程,求出方程的解,即可求出答案.
解答 解:如图,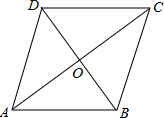
∵四边形ABCD是菱形,周长为20cm,
∴AB=BC=CD=AD=5cm,AC=2AO=2OC,BO=DO,AC⊥BD,
∴∠AOD=90°,
∵AC:BD=4:3,
∴AO:DO=4:3,
设AO=4xcm,DO=3xcm,
在△AOD中,由勾股定理得:AO2+DO2=AD2,
(3x)2+(4x)2=52,
解得:x=1,
∴AO=4cm,
∴AC=2AO=8cm,
故选C.
点评 本题考查了菱形对角线互相垂直平分的性质,注意菱形各边长相等的性质,勾股定理在直角三角形中的运用,本题中根据勾股定理求AO的值是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.如果a=(-99)0,b=(-0.1)-1,C=($-\frac{5}{3}$)-2,那么a、b、c的大小关系为( )
| A. | a>c>b | B. | c>a>b | C. | a>b>c | D. | c>b>a |
13.小数0.000314用科学记数法可表示为( )
| A. | 3.14×10-4 | B. | 3.14×10-5 | C. | 3.14×10-6 | D. | 3.14×10-7 |
18.一个多边形的内角和等于它的外角和的2倍,它是( )边形.
| A. | 五 | B. | 七 | C. | 六 | D. | 四 |
 如图,x=60,y=50.
如图,x=60,y=50. 已知∠1=∠4,∠3=∠5,∠B=∠2,求证:CE∥DF.
已知∠1=∠4,∠3=∠5,∠B=∠2,求证:CE∥DF.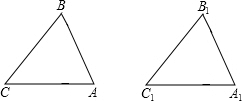 己知:△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1C1,∠C=∠C1
己知:△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1C1,∠C=∠C1