题目内容
17.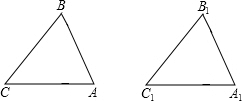 己知:△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1C1,∠C=∠C1
己知:△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1C1,∠C=∠C1求证:△ABC≌△A1B1C1.
分析 过B作BD⊥AC于D,过B1作B1D1⊥B1C1于D1,得出∠BDA=∠B1D1A1=∠BDC=∠B1D1C1=90°,根据SAS证△BDC≌△B1D1C1,推出BD=B1D1,根据HL证Rt△BDA≌Rt△B1D1A1,推出∠A=∠A1,根据AAS推出△ABC≌△A1B1C1即可.
解答 证明:过B作BD⊥AC于D,过B1作B1D1⊥B1C1于D1,
则∠BDA=∠B1D1A1=∠BDC=∠B1D1C1=90°,
在△BDC和△B1D1C1中
$\left\{\begin{array}{l}{∠C=∠{C}_{1}}\\{BC={B}_{1}{C}_{1}}\\{∠BDC=∠{B}_{1}{D}_{1}{C}_{1}}\end{array}\right.$
∴△BDC≌△B1D1C1,
∴BD=B1D1,
在Rt△BDA和Rt△B1D1A1中
$\left\{\begin{array}{l}{AB={A}_{1}{B}_{1}}\\{BD={B}_{1}{D}_{1}}\\{\;}\end{array}\right.$,
∴Rt△BDA≌Rt△B1D1A1(HL),
∴∠A=∠A1,
在△ABC和△A1B1C1中,
$\left\{\begin{array}{l}{∠C=∠{C}_{1}}\\{∠A=∠{A}_{1}}\\{AB={A}_{1}{B}_{1}}\end{array}\right.$,
∴△ABC≌△A1B1C1.
点评 本题考查了全等三角形的性质和判定的应用,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
8.菱形ABCD的周长为20cm,两条对角线AC:BD=4:3,那么对角线AC长( )
| A. | 5cm | B. | 6cm | C. | 8cm | D. | 10cm |
6.截止到2015年6月底,济南机动车总保有量为1640000辆,用科学记数法表示这个数为( )
| A. | 16.4×105 | B. | 1.64×105 | C. | 0.164×107 | D. | 1.64×106 |
7.已知一个立体图形的三视图如图所示,那么它是( )
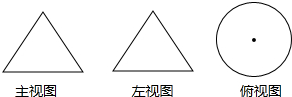

| A. | 圆锥 | B. | 球 | C. | 圆柱 | D. | 棱柱 |
 如图,∠DAC+∠ACB=180°,CE平分∠BCF,∠FEC=∠FCE,∠DAC=3∠BCF,∠ACF=20°.
如图,∠DAC+∠ACB=180°,CE平分∠BCF,∠FEC=∠FCE,∠DAC=3∠BCF,∠ACF=20°.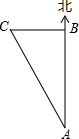 一艘在海上朝正北方向肮行的轮船,从点A到点B航行了240海里时方位仪坏了,凭经验,船长指挥船左转一定角度后,继续航行70海里后到达点C,此时AC之间的距离为250海里,你能判断船转弯后,是否沿正西方向航行?
一艘在海上朝正北方向肮行的轮船,从点A到点B航行了240海里时方位仪坏了,凭经验,船长指挥船左转一定角度后,继续航行70海里后到达点C,此时AC之间的距离为250海里,你能判断船转弯后,是否沿正西方向航行?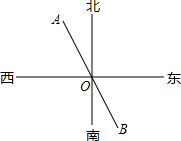 如图所示,已知点A,O,B在同一条直线上,若OA的方向是北偏西26°,则OB的方向是南偏东26°.
如图所示,已知点A,O,B在同一条直线上,若OA的方向是北偏西26°,则OB的方向是南偏东26°.