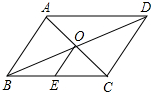如图.在平行四边形ABCD中.对角线AC.BD相交于点O.点E是边BC的中点.AB=4.则OE的长为( )A．$\sqrt{2}$B．1C．$\frac{1}{2}$D．2 题目和参考答案——青夏教育精英家教网—

题目内容

5．

如图，在平行四边形ABCD中，对角线AC，BD相交于点O，点E是边BC的中点，AB=4，则OE的长为（　　）

A．

$\sqrt{2}$

B．

C．

$\frac{1}{2}$

D．

分析因为四边形ABCD是平行四边形，所以OA=OC；再根据点E是BC的中点，得出OE是△ABC的中位线，由OE=1，即可求得AB=2．

解答解：∵四边形ABCD是平行四边形，
∴OA=OC；
又∵点E是BC的中点，
∴OE是△ABC的中位线，
∴根据三角形的中位线定理可得：AB=2OE=4．
则OE=2
故选：D．

点评此题考查了平行四边形的性质：平行四边形的对角线互相平分．还考查了三角形中位线的性质：三角形的中位线平行且等于三角形第三边的一半．

练习册系列答案

星空初中假期作业寒假乐园新疆青少年出版社系列答案

相关题目

15．在-3，2，0，-1这四个数中，大于0的数是（　　）

16．如果a＞b，下列各式中不正确的是（　　）

A．

a-1＞b-1

B．

$\frac{a}{2}$＞$\frac{b}{2}$

13．

如图，AB∥EF∥DC，EG∥DB，则图中与∠EGA相等的角共有5个．

20．解方程：x²-2x+$\frac{7}{{x}^{2}-2x}$=8．

10．解方程：$\sqrt{2}x-1=3-\sqrt{2}x$．

17．某体育场的一条环形跑道长400米，甲、乙两人从跑道上同一地点出发，分别以不变的速度练习长跑和骑自行车，如果背向而行，每隔$\frac{1}{2}$分钟他们相遇一次，如果同向而行，每隔1$\frac{1}{3}$分钟乙就追上甲一次，问：甲、乙每分钟各行多少米？

3．已知Rt△ABC中，AC=BC，∠C=90°，D为AB中点，∠EDF=90°，且∠EDF绕D点旋转，它的两边分别交AC、CB（或它们的延长线）于E、F．
（1）当∠EDF绕D点旋转到DE⊥AC时（图1），求证：${S_{△DEF}}+{S_{△CEF}}=\frac{1}{2}{S_{△ABC}}$．
（2）当∠EDF绕D点旋转到DE与AC不垂直．
①当两边与AC、BC相交时，（如图2），上述结论是否还会成立？若成立，请给予证明，若不成立，请说明理由．
②当两边与AC、BC的延长线相交时，（如图3），上述结论是否还会成立？若成立，请给予证明，若不成立，请说明S_△DEF、S_△CEF、S_△ABC之间的关系．（不需证明，直接回答即可）

4．

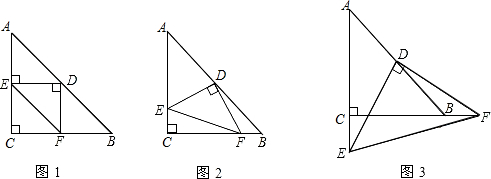
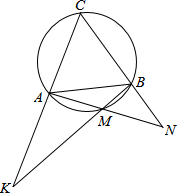如图，已知等边△ABC内接于圆，圆的半径为$\frac{\sqrt{3}}{2}$，在劣弧AB上取异于A、B的点M．如果设直线AC与BM相交于K，直线CB与AM相交于点N，则线段AK•BN的值为$\frac{9}{4}$．

试题分类