题目内容
18.如图,在平面直角坐标系中,直线y=2x+4$\sqrt{2}$与坐标轴分别交于A、B两点,点C在x轴上,且OA=OC,点P从A出发沿射线AC方向运动,速度为每秒1个单位长度,设运动时间为t(s).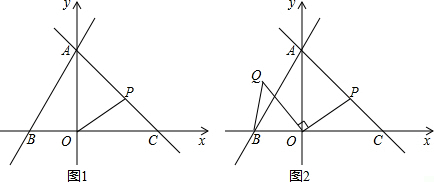
(1)求点B、C的坐标;
(2)若△OCP的面积为4,求运动时间t的值;
(3)如图2,若∠POQ=90°,且OP=OQ,连接BQ,求运动过程中BQ的最小值.
分析 (1)在y=2x+4$\sqrt{2}$中分别令x=0和y=0,则可求得A、B坐标,结合OA=OC可求得C点坐标;
(2)由条件可求得点O到直线AC的距离,用t可表示出PC的长,则可表示出△OCP的面积,可得到关于t的方程,可求得t的值;
(3)连接AQ,可证明△OQA≌△OPC,则可知∠OAQ=45°,可求得直线AQ的解析式,设直线AQ交x轴于点E,则当BQ⊥AE时,BQ最短,可求得BQ的长.
解答 解:
(1)在y=2x+4$\sqrt{2}$中,令x=0可得y=4$\sqrt{2}$,令y=0可得2x+4$\sqrt{2}$=0,解得x=-2$\sqrt{2}$,
∴A(0,4$\sqrt{2}$),B($-2\sqrt{2}$,0),
∴OC=OA=4$\sqrt{2}$,
∴C($4\sqrt{2}$,0);
(2)∵OA=OC=4$\sqrt{2}$,
∴AC=8,
∴点O到直线AC的距离为4,
当运动t秒时,则AP=t,则CP=|AP-AC|=|t-8|,
∴S△OCP=$\frac{1}{2}$×4|t-8|=2|t-8|,
∵△OCP的面积为4,
∴2|t-8|=4,解得t=6或t=10,
即当t为6秒或10秒时,△OCP的面积为4;
(3)如图,连接AQ,
∵∠POQ=90°,∠AOC=90°,
∴∠QOA+∠AOP=∠AOP+∠POC,
∴∠AOQ=∠COP,
在△OQA和△OPC中
$\left\{\begin{array}{l}{AO=CO}\\{∠AOQ=∠COP}\\{OQ=OP}\end{array}\right.$
∴△OQA≌△OPC(SAS),
∴∠OCP=∠OAQ=45°,
设直线AQ交y轴于点E,则E(-4$\sqrt{2}$,0),
∴BE=2$\sqrt{2}$,
设直线AQ解析式为y=kx+b,
∴$\left\{\begin{array}{l}{-4\sqrt{2}k+b=0}\\{b=4\sqrt{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{b=4\sqrt{2}}\end{array}\right.$,
∴直线AQ解析式为y=x+4$\sqrt{2}$,
∴点Q始终在直线$y=x+4\sqrt{2}$上,
∴BQ⊥AE时,BQ最短,
此时BQ=2,即BQ的最小值为2.
点评 本题为一次函数的综合应用,涉及函数与坐标轴的交点、三角形的面积、全等三角形的判定和性质、待定系数法、最短距离及方程思想等知识.在(2)中用t表示出△OCP的面积是解题的关键,在(3)中确定出点Q的位置是解题的关键.本题考查知识点较多,综合性较强,难度适中.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案 如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG.
如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG.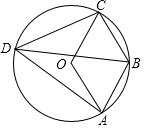 如图,四边形ABCD为⊙O的内接四边形,若四边形ABCO为平行四边形,则∠ADB=30°.
如图,四边形ABCD为⊙O的内接四边形,若四边形ABCO为平行四边形,则∠ADB=30°. 如图,矩形AOBC,A(0,3)、B(6,0),点E在OB上,∠AEO=30°,点P从点Q(-4,0)出发,沿x轴向右以每秒1个单位长的速度运动,运动时间为t秒.
如图,矩形AOBC,A(0,3)、B(6,0),点E在OB上,∠AEO=30°,点P从点Q(-4,0)出发,沿x轴向右以每秒1个单位长的速度运动,运动时间为t秒. ,当输出的数是10时,输入时的x=8.
,当输出的数是10时,输入时的x=8.