题目内容
10.已知a=3+$\sqrt{10}$,b=3-$\sqrt{10}$,求$\frac{b}{a}$+$\frac{a}{b}$的值.分析 先将$\frac{b}{a}$+$\frac{a}{b}$通分为$\frac{{b}^{2}+{a}^{2}}{ab}$,然后将a=3+$\sqrt{10}$,b=3-$\sqrt{10}$代入求解即可.
解答 解:∵a=3+$\sqrt{10}$,b=3-$\sqrt{10}$,
∴$\frac{b}{a}$+$\frac{a}{b}$
=$\frac{{b}^{2}}{ab}$+$\frac{{a}^{2}}{ab}$
=$\frac{{b}^{2}+{a}^{2}}{ab}$
=$\frac{9+10-6\sqrt{10}+9+10+6\sqrt{10}}{9-10}$
=-38.
点评 本题考查了分式的化简求值,解答本题的关键在于先将$\frac{b}{a}$+$\frac{a}{b}$通分为$\frac{{b}^{2}+{a}^{2}}{ab}$,然后将a=3+$\sqrt{10}$,b=3-$\sqrt{10}$代入求解.

练习册系列答案
相关题目
 一个圆锥的三视图如图所示,求圆锥的全面积.
一个圆锥的三视图如图所示,求圆锥的全面积.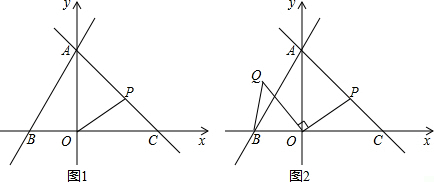
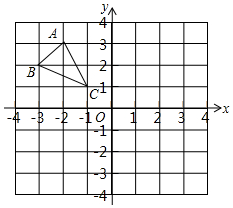 如图,在平面直角坐标中,△ABC各顶点都在小方格的顶点上.
如图,在平面直角坐标中,△ABC各顶点都在小方格的顶点上. 如图,在Rt△ABC中,∠A=90°,BE平分∠ABC,过点E作BC的垂线交BC于点D,CE=BE.求证:AB=CD.
如图,在Rt△ABC中,∠A=90°,BE平分∠ABC,过点E作BC的垂线交BC于点D,CE=BE.求证:AB=CD.