题目内容
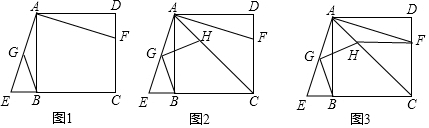
11. 如图是某水库大坝的横截面示意图,已知AD∥BC,且AD、BC之间的距离为15米,背水坡CD的坡度i=1:0.6,为提高大坝的防洪能力,需对大坝进行加固,加固后大坝顶端AE比原来的顶端AD加宽了2米,背水坡EF的坡度i=3:4,则大坝底端增加的长度CF是( )米.
如图是某水库大坝的横截面示意图,已知AD∥BC,且AD、BC之间的距离为15米,背水坡CD的坡度i=1:0.6,为提高大坝的防洪能力,需对大坝进行加固,加固后大坝顶端AE比原来的顶端AD加宽了2米,背水坡EF的坡度i=3:4,则大坝底端增加的长度CF是( )米.| A. | 7 | B. | 11 | C. | 13 | D. | 20 |
分析 过D作DG⊥BC于G,EH⊥BC于H,解直角三角形即可得到结论.
解答  解:过D作DG⊥BC于G,EH⊥BC于H,
解:过D作DG⊥BC于G,EH⊥BC于H,
∴GH=DE=2,
∵DG=EH=15,背水坡CD的坡度i=1:0.6,背水坡EF的坡度i=3:4,
∴CG=9,HF=20,
∴CF=GH+HF-CG=13米,
故选C.
点评 本题考查了解直角三角形的应用,解答本题的关键是理解坡度、坡比的含义,构造直角三角形,利用三角函数表示相关线段的长度,难度一般.

练习册系列答案
相关题目
20.某公司需要从甲、乙两个仓库向A、B两地分别运送100t和50t的物资.已知该物资在甲仓库有80t,乙仓库有70t.从甲、乙两个仓库运送物资到A、B两地的运费如下表:
(1)设从甲仓库运送到A地的物资为xt,求运送的总运费y(单位:元)与x(单位:t)之间的函数解析式,并写出x的取值范围.
(2)请你设计出运费最低的运送方案,并求出最低运费.
| 目的地 | 运费/(元/t) | |
| 甲仓库 | 乙仓库 | |
| A地 | 140 | 200 |
| B地 | 100 | 80 |
(2)请你设计出运费最低的运送方案,并求出最低运费.
1.若a+b=3,则代数式($\frac{{b}^{2}}{a}$-a)÷$\frac{a-b}{a}$的值为( )
| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
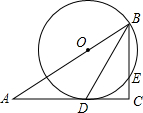 如图,在Rt△ABC中,C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
如图,在Rt△ABC中,C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.