题目内容
19.将背面相同,正面分别标有数字1、2、3、4的四张卡片洗匀后,背面朝上放在桌子上.请用树状图或列表法解答下列问题:(1)从中随机抽取两张卡片,求卡片正面上的数字之积大于4的概率;
(2)若先从中随机抽取一张卡片(不放回),将该卡片正面上的数字作为十位上的数字;再随机抽取一张,将该卡片正面上的数字作为个位上的数字,求组成的两位数恰好是3的倍数的概率.
分析 (1)画树状图展示所有12种等可能的结果数,找出卡片正面上的数字之积大于4的结果数,然后根据概率公式求解;
(2)利用树状图得到共有12种等可能的结果数,再找出组成的两位数恰好是3的倍数的结果数,然后根据概率公式求解.
解答 解:(1)画树状图为:
共有12种等可能的结果数,其中卡片正面上的数字之积大于4的结果数为6,
所以卡片正面上的数字之积大于4的概率=$\frac{6}{12}$=$\frac{1}{2}$;
(2)共有12种等可能的结果数,其中组成的两位数恰好是3的倍数有4种情况,
所以组成的两位数恰好是3的倍数的概率=$\frac{4}{12}$=$\frac{1}{3}$.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10. 如图,Rt△ACB中,∠C=90°,AC=12,BC=5,等腰Rt△DEF的顶点D、E分别在边AC、AB上,且ED⊥AC于点D,连接AF并延长交BC于点G.已知DE=EF=2,则BG的长为( )
如图,Rt△ACB中,∠C=90°,AC=12,BC=5,等腰Rt△DEF的顶点D、E分别在边AC、AB上,且ED⊥AC于点D,连接AF并延长交BC于点G.已知DE=EF=2,则BG的长为( )
 如图,Rt△ACB中,∠C=90°,AC=12,BC=5,等腰Rt△DEF的顶点D、E分别在边AC、AB上,且ED⊥AC于点D,连接AF并延长交BC于点G.已知DE=EF=2,则BG的长为( )
如图,Rt△ACB中,∠C=90°,AC=12,BC=5,等腰Rt△DEF的顶点D、E分别在边AC、AB上,且ED⊥AC于点D,连接AF并延长交BC于点G.已知DE=EF=2,则BG的长为( )| A. | $\frac{25}{17}$ | B. | $\frac{30}{17}$ | C. | $\frac{17}{12}$ | D. | $\frac{19}{12}$ |
11. 如图是某水库大坝的横截面示意图,已知AD∥BC,且AD、BC之间的距离为15米,背水坡CD的坡度i=1:0.6,为提高大坝的防洪能力,需对大坝进行加固,加固后大坝顶端AE比原来的顶端AD加宽了2米,背水坡EF的坡度i=3:4,则大坝底端增加的长度CF是( )米.
如图是某水库大坝的横截面示意图,已知AD∥BC,且AD、BC之间的距离为15米,背水坡CD的坡度i=1:0.6,为提高大坝的防洪能力,需对大坝进行加固,加固后大坝顶端AE比原来的顶端AD加宽了2米,背水坡EF的坡度i=3:4,则大坝底端增加的长度CF是( )米.
 如图是某水库大坝的横截面示意图,已知AD∥BC,且AD、BC之间的距离为15米,背水坡CD的坡度i=1:0.6,为提高大坝的防洪能力,需对大坝进行加固,加固后大坝顶端AE比原来的顶端AD加宽了2米,背水坡EF的坡度i=3:4,则大坝底端增加的长度CF是( )米.
如图是某水库大坝的横截面示意图,已知AD∥BC,且AD、BC之间的距离为15米,背水坡CD的坡度i=1:0.6,为提高大坝的防洪能力,需对大坝进行加固,加固后大坝顶端AE比原来的顶端AD加宽了2米,背水坡EF的坡度i=3:4,则大坝底端增加的长度CF是( )米.| A. | 7 | B. | 11 | C. | 13 | D. | 20 |
8.下列说法中,正确的是( )
| A. | 一个游戏中奖的概率是$\frac{1}{10}$,则做10次这样的游戏一定会中奖 | |
| B. | 为了了解一批炮弹的杀伤半径,应采用全面调查的方式 | |
| C. | 一组数据8,7,7,10,6,7,9的众数和中位数都是7 | |
| D. | 若甲组数据的方差是0.1,乙组数据的方差是0.2,则乙组数据比甲组数据波动小 |
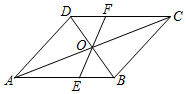 如图所示,在?ABCD中,对角线AC与BD相交于点O,过点O作一条直线分别交AB,CD于点E,F.
如图所示,在?ABCD中,对角线AC与BD相交于点O,过点O作一条直线分别交AB,CD于点E,F.