题目内容
20．已知a+b=3，ab=-4，则a2b+ab2的值为-12．分析 直接提取公因式ab，进而将已知代入求出即可．
解答 解：∵a+b=3，ab=-3，
∴a2b+ab2=ab（a+b）=4×（-3）=-12．
故答案为：-12
点评 此题主要考查了提取公因式法分解因式，正确找出公因式是解题关键．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
2．下列各式正确的是（ ）
| A． | $\sqrt{4\frac{4}{9}}=2\frac{2}{3}$ | B． | $\frac{{\sqrt{12}}}{3}=2$ | C． | $\sqrt{3}+\sqrt{2}=\frac{1}{{\sqrt{3}-\sqrt{2}}}$ | D． | $\sqrt{{{（-3）}^2}}=-3$ |
3．
如图，在⊙O中，OC⊥弦AB于点C，AB=6，OC=1，则OB的长是（ ）
如图，在⊙O中，OC⊥弦AB于点C，AB=6，OC=1，则OB的长是（ ）| A． | $\sqrt{3}$ | B． | $\sqrt{5}$ | C． | $\sqrt{10}$ | D． | 4 |
8．已知⊙O的半径为3cm，点P在⊙O内，则OP不可能等于（ ）
| A． | 1cm | B． | 1.5cm | C． | 2cm | D． | 3cm |
15．已知x=y，a是任意数，则下列结论错误的是（ ）
| A． | a-x=a-y | B． | x-y=0 | C． | ax=ay | D． | $\frac{x}{a+1}$=$\frac{y}{a+1}$ |
5．
已知如图，CO、CB是⊙O′的弦，⊙O′与坐标系x、y轴交于B、A两点，点A的坐标为（0，1），⊙O′的弦OB的长为$\sqrt{3}$，则∠OCB的度数为（ ）
已知如图，CO、CB是⊙O′的弦，⊙O′与坐标系x、y轴交于B、A两点，点A的坐标为（0，1），⊙O′的弦OB的长为$\sqrt{3}$，则∠OCB的度数为（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 75° |
12．p+q=0，抛物线y=x2+px+q必经过（ ）
| A． | （-1，1） | B． | （1，-1） | C． | （-1，-1） | D． | （1，1） |
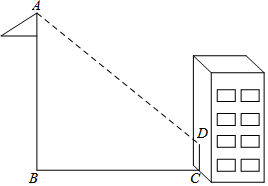数学兴趣小组的同学们，想利用自己所学的数学知识测量学校旗杆的高度：下午活动时间，兴趣小组的同学们来到操场，发现旗杆的影子有一部分落在了墙上（如图所示）．同学们按照以下步骤进行测量：测得小明的身高1.65米，此时其影长为2.5米；在同一时刻测量旗杆影子落在地面上的影长BC为9米，留在墙上的影高CD为2米，请你帮助兴趣小组的同学们计算旗杆的高度．