题目内容
3．
如图，在⊙O中，OC⊥弦AB于点C，AB=6，OC=1，则OB的长是（ ）| A． | $\sqrt{3}$ | B． | $\sqrt{5}$ | C． | $\sqrt{10}$ | D． | 4 |
分析 先根据垂径定理得到BC=AC=3，然后根据勾股定理可计算出OB．
解答 解：∵OC⊥弦AB于点C，
∴BC=AC=$\frac{1}{2}$AB=$\frac{1}{2}$×6=3，
在Rt△OBC中，OC=1，BC=3，
∴OB=$\sqrt{O{C}^{2}+B{C}^{2}}$=$\sqrt{10}$，
故选：C．
点评 本题考查了垂径定理：平分弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了勾股定理．
练习册系列答案
相关题目
13．一个点从数轴上的原点出发，向左移动3个单位长度，再向右移动2个单位长度到达点P，则点P表示的数是（ ）
| A． | 1 | B． | -1 | C． | 2 | D． | -2 |
14．随机掷一枚质地均匀的硬币两次，落地后两次都是反面朝上的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{3}{4}$ |
11．
如图是一个正方体展开图，把展开图折叠成正方体后，与“美”字相对的面上的汉字是（ ）
如图是一个正方体展开图，把展开图折叠成正方体后，与“美”字相对的面上的汉字是（ ）| A． | 的 | B． | 中 | C． | 国 | D． | 梦 |
18．
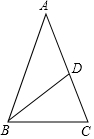如图，等腰三角形ABC中，AB=AC，BD平分∠ABC，∠A=36°，则∠BDC的度数为（ ）
如图，等腰三角形ABC中，AB=AC，BD平分∠ABC，∠A=36°，则∠BDC的度数为（ ）| A． | 36° | B． | 60° | C． | 108° | D． | 72° |
8．
有理数a，b在数轴上的对应的位置如图所示，则（ ）
有理数a，b在数轴上的对应的位置如图所示，则（ ）| A． | a+b＜0 | B． | a-b＞0 | C． | a-b=0 | D． | ab＞0 |
1．
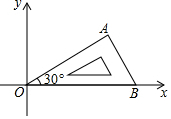将含有30°角的直角三角板OAB如图放置在平面直角坐标中，OB在x轴上，若OA=2，将三角板绕原点O顺时针旋转75°，则点A的对应点A′的坐标为（ ）
将含有30°角的直角三角板OAB如图放置在平面直角坐标中，OB在x轴上，若OA=2，将三角板绕原点O顺时针旋转75°，则点A的对应点A′的坐标为（ ）| A． | （$\sqrt{3}$，1） | B． | （1，-$\sqrt{3}$） | C． | （$\sqrt{2}$，-$\sqrt{2}$） | D． | （-$\sqrt{2}$，$\sqrt{2}$） |