题目内容
12．p+q=0，抛物线y=x2+px+q必经过（ ）| A． | （-1，1） | B． | （1，-1） | C． | （-1，-1） | D． | （1，1） |
分析 将x=1代入y=x2+px+q，得y=1+p+q，即y=1，由此确定选择项．
解答 解：∵y=x2+px+q，
∴当x=1时，y=1+p+q，
又∵p+q=0，
∴y=1，
即抛物线y=x2+px+q必过点（1，1）．
故选D．
点评 本题考查二次函数图象上点的坐标特征，图象经过点，点的坐标一定满足函数的解析式．
练习册系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
14．随机掷一枚质地均匀的硬币两次，落地后两次都是反面朝上的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{3}{4}$ |
如图，在△ABC中，∠C=90°，AB=8，cosB=$\frac{3}{4}$，则BC的长是6．
1．
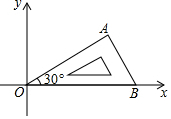将含有30°角的直角三角板OAB如图放置在平面直角坐标中，OB在x轴上，若OA=2，将三角板绕原点O顺时针旋转75°，则点A的对应点A′的坐标为（ ）
将含有30°角的直角三角板OAB如图放置在平面直角坐标中，OB在x轴上，若OA=2，将三角板绕原点O顺时针旋转75°，则点A的对应点A′的坐标为（ ）| A． | （$\sqrt{3}$，1） | B． | （1，-$\sqrt{3}$） | C． | （$\sqrt{2}$，-$\sqrt{2}$） | D． | （-$\sqrt{2}$，$\sqrt{2}$） |
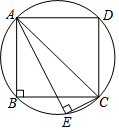如图，正方形ABCD内接于⊙O，AD=2，弦AE平分BC交BC于P，连接CE，则CE的长为$\frac{2\sqrt{5}}{5}$．