题目内容
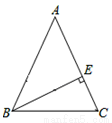
4. 如图,在Rt△ABC中,∠C=90°,AC=6,BC=3,P为AC上一个动点,PCEF为矩形,其中点E、F分别在BC、AB上.若矩形PCEF的周长等于10,求AP的长.
如图,在Rt△ABC中,∠C=90°,AC=6,BC=3,P为AC上一个动点,PCEF为矩形,其中点E、F分别在BC、AB上.若矩形PCEF的周长等于10,求AP的长.
分析 由矩形的性质可知:EF∥DC,所以△BFE∽△BCA,由相似三角形的性质求出CP的长,即可求出结论.
解答 解:∵四边形EFCD是矩形,
∴EF∥PC,EF=CP,CE=PF,
∵矩形PCEF的周长等于10,
设EF=CP=x,则CE=5-x,BE=x-2,
∵EF∥PC,
∴△BFE∽△BCA,
∴$\frac{EF}{AC}=\frac{BE}{BC}$,即$\frac{x}{6}=\frac{x-2}{3}$,
∴x=4,
∴EF=CP=4,
∴AP=2.
点评 本题考查了矩形的性质和相似三角形的判定以及性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
14.出租车司机小王驾车在东西方向的街道上行驶,如果把最初的出发点记作0,向东行驶记作正,向西行驶记作负,某天上午行驶的路程如下表(单位:km):
(1)到中午,小王是否回到了最初的出发点?
(2)小王距离最初的出发点最远是多少千米?
(3)小王在上述过程中一共行驶了多少路程?
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 路程 | +5 | -3 | +10 | -8 | -6 | +12 | -10 |
(2)小王距离最初的出发点最远是多少千米?
(3)小王在上述过程中一共行驶了多少路程?
12. 如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC=( )
如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC=( )
 如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC=( )
如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC=( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
19. 如图,数轴上的A,B两点分别表示有理数a,b,则在下列各式中,不成立的是( )
如图,数轴上的A,B两点分别表示有理数a,b,则在下列各式中,不成立的是( )
 如图,数轴上的A,B两点分别表示有理数a,b,则在下列各式中,不成立的是( )
如图,数轴上的A,B两点分别表示有理数a,b,则在下列各式中,不成立的是( )| A. | a<b | B. | -a>b | C. | |a|<|b| | D. | -a>-b |
 如图,在△ABC中,AB=AC,点P是边BC上任意一点,求证:AB2-AP2=BP•CP.
如图,在△ABC中,AB=AC,点P是边BC上任意一点,求证:AB2-AP2=BP•CP.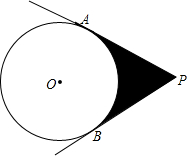 如图,PA、PB为⊙O的切线,⊙O的半径为2,∠P=60°.阴影部分的周长是$\frac{4}{3}$π+4$\sqrt{3}$,面积是4$\sqrt{3}$-$\frac{4}{3}$π.
如图,PA、PB为⊙O的切线,⊙O的半径为2,∠P=60°.阴影部分的周长是$\frac{4}{3}$π+4$\sqrt{3}$,面积是4$\sqrt{3}$-$\frac{4}{3}$π.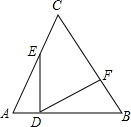 如图,等边△ABC的边长为8,E为AC上一动点,ED⊥AB于D,DF⊥BC于F.
如图,等边△ABC的边长为8,E为AC上一动点,ED⊥AB于D,DF⊥BC于F.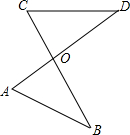 如图所示,AD与BC相交于点O,且$\frac{OA}{OC}$=$\frac{OB}{OD}$,若OA=1.5,OC=2,AB=3,则CD的长为4.
如图所示,AD与BC相交于点O,且$\frac{OA}{OC}$=$\frac{OB}{OD}$,若OA=1.5,OC=2,AB=3,则CD的长为4.