题目内容
9.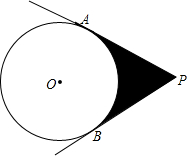 如图,PA、PB为⊙O的切线,⊙O的半径为2,∠P=60°.阴影部分的周长是$\frac{4}{3}$π+4$\sqrt{3}$,面积是4$\sqrt{3}$-$\frac{4}{3}$π.
如图,PA、PB为⊙O的切线,⊙O的半径为2,∠P=60°.阴影部分的周长是$\frac{4}{3}$π+4$\sqrt{3}$,面积是4$\sqrt{3}$-$\frac{4}{3}$π.
分析 连结OA、OB、OP,如图,根据切线的性质和切线长定理得到OA⊥PA,OB⊥PB,PA=PB,OP平分∠APB,则∠AOB=180°-∠APB=120°,∠APO=$\frac{1}{2}$∠APB=30°,利用弧长公式可计算出弧AB的长=$\frac{4}{3}$π,利用扇形面积公式可计算出扇形AOB的面积=$\frac{4}{3}$π,接着在Rt△AOP中利用含30度的直角三角形三边的关系可得PA=$\sqrt{3}$OA=2$\sqrt{3}$,则S△AOP=2$\sqrt{3}$,然后计算弧AB、PA、PB的和得到阴影部分的周长,计算2S△AOP-S扇形AOB得到阴影部分的面积.
解答 解:连结OA、OB、OP,如图,
∵PA、PB为⊙O的切线,
∴OA⊥PA,OB⊥PB,PA=PB,OP平分∠APB,
∴∠AOB=180°-∠APB=180°-60°=120°,∠APO=$\frac{1}{2}$∠APB=30°,
∴弧AB的长=$\frac{120•π•2}{180}$=$\frac{4}{3}$π,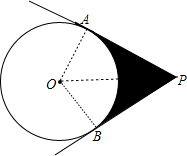
扇形AOB的面积=$\frac{120•π•{2}^{2}}{360}$=$\frac{4}{3}$π,
在Rt△AOP中,∵∠APO=30°,
∴PA=$\sqrt{3}$OA=2$\sqrt{3}$,
∴S△AOP=$\frac{1}{2}$•2•2$\sqrt{3}$=2$\sqrt{3}$,
∴阴影部分的周长=$\frac{4}{3}$π+2$\sqrt{3}$+2$\sqrt{3}$=$\frac{4}{3}$π+4$\sqrt{3}$
阴影部分的面积=2S△AOP-S扇形AOB=2×2$\sqrt{3}$-$\frac{4}{3}$π=4$\sqrt{3}$-$\frac{4}{3}$π.
故答案为$\frac{4}{3}$π+4$\sqrt{3}$;4$\sqrt{3}$-$\frac{4}{3}$π.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了弧长公式和扇形的面积公式.

| A. | 圆的面积S和半径R之间的关系 | |
| B. | 匀速行驶的汽车,行驶的路程s与时间t之间的关系 | |
| C. | 一个正数的平方根与它本身之间的关系 | |
| D. | 电阻一定,加在这个电阻两端的电压通过这个电阻的电流之间的关系 |
 如图,在Rt△ABC中,∠C=90°,AC=6,BC=3,P为AC上一个动点,PCEF为矩形,其中点E、F分别在BC、AB上.若矩形PCEF的周长等于10,求AP的长.
如图,在Rt△ABC中,∠C=90°,AC=6,BC=3,P为AC上一个动点,PCEF为矩形,其中点E、F分别在BC、AB上.若矩形PCEF的周长等于10,求AP的长. 如图,△ABC中,∠C=90°,CA=CB,D是AB的中点,AE=CF.
如图,△ABC中,∠C=90°,CA=CB,D是AB的中点,AE=CF. 八年级(6)班的同学做游戏,在活动区放了一些球(如图),小明应按怎样的路线跑,去捡起那个位置的球,才能最快拿到球跑到目的地A?
八年级(6)班的同学做游戏,在活动区放了一些球(如图),小明应按怎样的路线跑,去捡起那个位置的球,才能最快拿到球跑到目的地A? 的解集为
的解集为 ,则
,则 的取值范围是 __________
的取值范围是 __________