题目内容
16.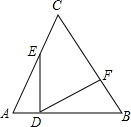 如图,等边△ABC的边长为8,E为AC上一动点,ED⊥AB于D,DF⊥BC于F.
如图,等边△ABC的边长为8,E为AC上一动点,ED⊥AB于D,DF⊥BC于F.(1)若CE=2,求CF的长;
(2)当CE取何值时,DE=DF?
分析 (1)因为AC=8,CE=2,所以AE=AC-CE=6,又因为在Rt△AED中∠AED=90°-∠A=30°,根据直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半可得AD=$\frac{1}{2}$AE=3,所以BD=AB-AD=5,同理可知,在Rt△BFD中∠BDF=90°-∠B=30°,BF=$\frac{1}{2}$BD=$\frac{5}{2}$,CF=BC-FB=$\frac{11}{2}$,则可根据CF=BC-FB求得结果;
(2)根据AAS证得△BDE≌△CFE,则有AD=BF=$\frac{1}{2}$BD,AD=$\frac{1}{3}$AB=$\frac{8}{3}$,AE=2AD=$\frac{16}{3}$,则有CE=AC-AE=$\frac{8}{3}$时,DE=DF.
解答 解:(1)∵AC=8,CE=2,
∴AE=AC-CE=6,
在Rt△AED中,
∠AED=90°-∠A=30°,
∴AD=$\frac{1}{2}$AE=3,
∴BD=AB-AD=5,
在Rt△BFD中
∠BDF=90°-∠B=30°,
∴BF=$\frac{1}{2}$BD=$\frac{5}{2}$,
∴CF=BC-FB=$\frac{11}{2}$;
(2)在△AED和△DFB中,
$\left\{\begin{array}{l}{∠ADE=∠BFD}\\{∠A=∠B}\\{DE=DF}\end{array}\right.$,
∴△AED≌△BDF(AAS)
∴AD=BF,
∴AD=BF=$\frac{1}{2}$BD,
∴AD=$\frac{1}{3}$AB=$\frac{8}{3}$,
∴AE=2AD=$\frac{16}{3}$,
∴CE=AC-AE=$\frac{8}{3}$,
∴CE=$\frac{8}{3}$时,DE=DF.
点评 本题把全等三角形的判定和性质结合求解,考查学生综合运用数学知识的能力.充分掌握和理解直角三角形中的一些特殊的对应关系并灵活运用可解得此题.

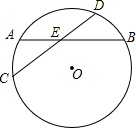 如图,⊙0的弦CD平分AB,交点为E.
如图,⊙0的弦CD平分AB,交点为E. 如图,在Rt△ABC中,∠C=90°,AC=6,BC=3,P为AC上一个动点,PCEF为矩形,其中点E、F分别在BC、AB上.若矩形PCEF的周长等于10,求AP的长.
如图,在Rt△ABC中,∠C=90°,AC=6,BC=3,P为AC上一个动点,PCEF为矩形,其中点E、F分别在BC、AB上.若矩形PCEF的周长等于10,求AP的长.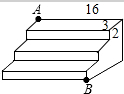 如图,是一个三级台阶,它的每一级的长、宽、高分别为16dm,3dm,2dm,A和B是这个台阶两相对的端点,A点有一只昆虫想到B点去吃可口的食物,则昆虫沿着台阶爬到B点最短路程是多少dm?
如图,是一个三级台阶,它的每一级的长、宽、高分别为16dm,3dm,2dm,A和B是这个台阶两相对的端点,A点有一只昆虫想到B点去吃可口的食物,则昆虫沿着台阶爬到B点最短路程是多少dm? 如图,求作一点P,使PA=PB,PC=PD(只保留作图痕迹,不要求写出作法)
如图,求作一点P,使PA=PB,PC=PD(只保留作图痕迹,不要求写出作法)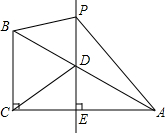 如图,在△ABC中,当∠ACB=90°,∠BAC=30°,BC=$\sqrt{3}$,过AB的中点D作DE⊥AC,垂足为点E,点P是直线DE上一动点,连结AP,BP,CD
如图,在△ABC中,当∠ACB=90°,∠BAC=30°,BC=$\sqrt{3}$,过AB的中点D作DE⊥AC,垂足为点E,点P是直线DE上一动点,连结AP,BP,CD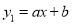 与
与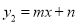 相交于点
相交于点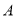 (2,
(2, 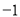 ),若
),若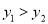 ,则
,则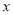 的取值范围是( )
的取值范围是( )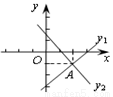
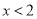 B.
B. 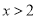 C.
C. 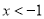 D.
D. 