题目内容
6．若实数m，n 满足m2-m+$\frac{1}{4}$+|n+2017|=0，则m-2-n0=3．分析 根据非负数的和等于零，可得n，m的值，根据负整数指数幂与正整数指数幂互为倒数，零次幂，可得答案．
解答 解：由题意，得
（m-$\frac{1}{2}$）2+|n+2017|=0，
解得m=$\frac{1}{2}$，n=-2017．
m-2-n0=4-1=3，
故答案为：3．
点评 本题考查了非负数的性质，利用据非负数的和等于零得出n，m的值是解题关键．
练习册系列答案
相关题目
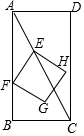如图，在矩形ABCD中，AB=4，BC=2，点E从点A出发，以每秒$\sqrt{5}$个单位长度的速度沿对角线AC向终点C运动，点F从点B出发，以每秒2个单位长度的速度沿边BA向终点A运动，连结EF，将线段EF绕点F顺时针旋转90°得到线段FG，以EF，FG为边作正方形EFGH，设点E运动的时间为t秒（t＞0）．
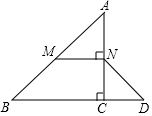如图，在△ABC中，∠ACB=90°，M、N分别是AB、AC的中点，延长BC至点D，使CD=$\frac{1}{3}$BD，连接DN、MN．若AB=6．