题目内容
11．已知关于x的一元二次方程x2-（m+2）x+2m=0．（1）求证：方程总有两个实数根；
（2）当m=2时，求方程的两个根．
分析 （1）证明△≥0即可；
（2）把m=2代入方程得到x2-4x+4=0，然后利用配方法解方程即可．
解答 （1）证明：∵△=[-（m+2）]2-4×2m1
=（m-2）2?
∵（m-2）2≥0，
∴方程总有两个实数根．2
（2）当m=2时，原方程变为x2-4x+4=0，
解得x1=x2=2．
点评 本题考查了根的判别式：一元二次方程ax2+bx+c=0（a≠0）的根与△=b2-4ac有如下关系：当△＞0时，方程有两个不相等的两个实数根；当△=0时，方程有两个相等的两个实数根；当△＜0时，方程无实数根．
练习册系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
2．已知a+$\frac{1}{a}$=$\sqrt{6}$，则a-$\frac{1}{a}$的值为（ ）
| A． | $\sqrt{2}$ | B． | ±$\sqrt{2}$ | C． | 2 | D． | ±2 |
如图，在?ABCD中，过点A作AE⊥BC于点E，AF⊥DC于点F，AE=AF．
如图，将一张矩形纸片ABCD沿直线MN折叠，使点C落在点A处，点D落在点E处，直线MN交BC于点M，交AD于点N．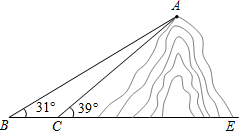
如图，小明想测山高度，他在B处仰望山顶A，测得仰角∠B=31°，再往山的方向（水平方向）前进80m至索道口C处，沿索道方向仰望山顶，测得仰角∠ACE=39°．求这座山的高度（小明的身高忽略不计）．