题目内容
15.已知反比例函数y=$\frac{k}{x}$过点A(1,.4).(1)求反比例函数的解析式;
(2)若该反比例函数的图象与直线y=mx+4(m≠0)只有一个公共点,求m的值.
分析 (1)将点A(1,4)代入解析式求得k的值即可得;
(2)解方程组得到kx2+4x-4=0,由反比例函数的图象与直线y=kx+4(k≠0)只有一个公共点,得到△=16+16k=0,求得k=-1.
解答 解:(1)将点A(1,4)代入解析式得:k=4,
∴反比例函数解析式为y=$\frac{4}{x}$;
(2)解$\left\{\begin{array}{l}{y=\frac{4}{x}}\\{y=mx+4}\end{array}\right.$得mx2+4x-4=0,
∵反比例函数的图象与直线y=mx+4(m≠0)只有一个公共点,
∴△=16+16m=0,
∴m=-1.
点评 本题考查了反比例函数与一次函数的交点问题,一元二次方程根与系数的关系,知道反比例函数的图象与直线y=mx+4(m≠0)只有一个公共点时,△=0是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.下列式子运算结果为x+1的是( )
| A. | $\frac{{x}^{2}-1}{x}$$•\frac{x}{x+1}$ | B. | 1-$\frac{1}{x}$ | C. | $\frac{{x}^{2}+2x+1}{x+1}$ | D. | $\frac{x+1}{x}$÷$\frac{1}{x-1}$ |
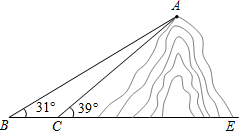 如图,小明想测山高度,他在B处仰望山顶A,测得仰角∠B=31°,再往山的方向(水平方向)前进80m至索道口C处,沿索道方向仰望山顶,测得仰角∠ACE=39°.求这座山的高度(小明的身高忽略不计).
如图,小明想测山高度,他在B处仰望山顶A,测得仰角∠B=31°,再往山的方向(水平方向)前进80m至索道口C处,沿索道方向仰望山顶,测得仰角∠ACE=39°.求这座山的高度(小明的身高忽略不计).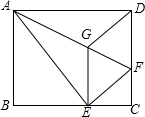 如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.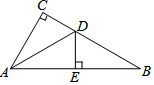 如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E,若AC=3cm,AB=5cm,则DE=$\frac{3}{2}$cm.
如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E,若AC=3cm,AB=5cm,则DE=$\frac{3}{2}$cm.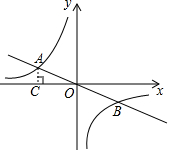 如图,双曲线y=$\frac{k}{x}$(k≠0)和直线y=$-\frac{1}{3}x$在第二、四象限分别交于A,B,过点A作AC⊥x轴于点C.已知点B的横坐标为3.
如图,双曲线y=$\frac{k}{x}$(k≠0)和直线y=$-\frac{1}{3}x$在第二、四象限分别交于A,B,过点A作AC⊥x轴于点C.已知点B的横坐标为3.