��Ŀ����
1����1����ͼ1���߶�AB�ij�Ϊ4����������һ����ABΪб�����������ֱ��������ABC����2����ͼ2�����ı���ABCD�У�AD=CD����ABC=120�㣬��ADC=60�㣬AB=4��BC=2����������ı���ABCD�������
��������
��3��С���ְ����ڵĹ�����Ҫ��ȡij���ı��εIJ��ϰ壬���ֲ��ϰ����״��ͼ3��ʾ�������������ı���ABCD�У�AD=CD����ABC=75�㣬��ADC=60�㣬DB=4��������������ı����������Сֵ������ܣ��������ʱ�ı���ABCD�������Сֵ��������ܣ���˵�����ɣ�
���� ��1������90���Բ�ܽ����Ե�����ֱ������O�����ɵױ�ABһ��ʱ�������ʱ��ֱ��������ABC��������ȷ����C��λ�ã�
��2���������ߣ����ı���ABCD�ֳɵȱ������κͶ۽������Σ�������������ı���ABCD��������ɣ�
��3��������ת�������������ߣ������ȱߡ�BHD���������ABH��������ֵ����ȷ���ı���ABCD�������Сֵ����ABH��������ֵ���ã�1���Ľ��ۣ�������Բ�ɵó����Ӷ��ó����ۣ�
��� �⣺��1����ͼ1��
��������ABΪֱ����ԲO������Cλ�ڰ�Բ���е�ʱ��ֱ�ǡ�ABC��������
��2�� ��ͼ2������AC����C��CH��AB����AB���ӳ�����H��
��ͼ2������AC����C��CH��AB����AB���ӳ�����H��
��Rt��BCH�У���BC=2����CBH=180��-120��=60�㣬
���BCH=30�㣬
��BH=$\frac{1}{2}$BC=1��HC=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$��
��AH=AB+BH=4+1=5��
��Rt��ACH��AC2=AH2+CH2=52+��$\sqrt{3}$��2=28��
��S��ABC=$\frac{1}{2}$AB•CH=$\frac{1}{2}$��4��$\sqrt{3}$=2$\sqrt{3}$��
��AD=CD����ADC=60�㣬
���ADC�ǵȱ������Σ�
��S��ADC=$\frac{\sqrt{3}}{4}$AC2=$\frac{\sqrt{3}}{4}$��28=7$\sqrt{3}$��
��S�ı���ABCD=S��ABC+S��ACD=2$\sqrt{3}$+7$\sqrt{3}$=9$\sqrt{3}$��
��3���ܣ�
��ͼ3������AC��
��AD=CD����ADC=60�㣬
���ADC�ǵȱ������Σ�
����BDC�Ƶ�D˳ʱ����ת60��á�HDA������BH��
��BD=DH=4����HDB=60�㣬
���HDB�ǵȱ������Σ�
��S�ı���ABCD=S��ABD+S��BCD
=S��BDH-S��ABH��
��BD=4���Ƕ�ֵ��
��S��BDH�Ƕ�ֵ��
�൱��ABH��������ʱ���ı���ABCD�������С��
�ߡ�ABC=75�㣬��ADC=60�㣬
���BAD+��BCD=360��-75��-60��=225�㣬
���BAH=360��-��BAD-��HAD=360��-225��=135�㣬
��BH=BD=4��
���A�ڶ�Բ��O����ABH�����Բ�����˶�����O��A��D����ʱ����ABH��������ʱ��OD��BH��
��OA��BH��K����HK=KB=2��
��AH=AB��
���AHB=��ABH=22.5�㣬
��HK��ȡһ��F��ʹFH=AF�����AKF�ǵ���ֱ�������Σ�
��AK=FK=x����AF=FH=$\sqrt{2}$x��
��2=x+$\sqrt{2}$x��
��x=2$\sqrt{2}$-2��
���ABH��������ֵ=$\frac{1}{2}$��4��$��2\sqrt{2}-2��$=4$\sqrt{2}$-4��
���ı���ABCD���������Сֵ=$\frac{\sqrt{3}}{4}$��42-��4$\sqrt{2}$-4��=4$\sqrt{3}$-4$\sqrt{2}$+4��
���� �������ı��ε��ۺ��⣬������Բ�ܽǶ���������ֱ�������ε����ʣ��ı��κ����������������ת�����ʡ��ȱ������ε����ʺ������ʽ��S=$\frac{\sqrt{3}}{4}$���߳���ƽ�������������Ѷȣ������������ǹؼ��������ڡ�ABH��������ֵ��ȷ���ı����������Сֵ����һ���ѵõļ���ѹ���⣮

 Ӣ�ŵ��ϵ�д�
Ӣ�ŵ��ϵ�д� ������������Ծ�ϵ�д�
������������Ծ�ϵ�д� ��ͼ���ڡ�ABC�У�AB=AC������A��AD��BC������1=50�㣬���CAD�Ĵ�СΪ��������
��ͼ���ڡ�ABC�У�AB=AC������A��AD��BC������1=50�㣬���CAD�Ĵ�СΪ��������| A�� | 50�� | B�� | 65�� | C�� | 80�� | D�� | 60�� |
| A�� | $\frac{{x}^{2}-1}{x}$$•\frac{x}{x+1}$ | B�� | 1-$\frac{1}{x}$ | C�� | $\frac{{x}^{2}+2x+1}{x+1}$ | D�� | $\frac{x+1}{x}$��$\frac{1}{x-1}$ |
 ��ͼ����?ABCD�У�����A��AE��BC�ڵ�E��AF��DC�ڵ�F��AE=AF��
��ͼ����?ABCD�У�����A��AE��BC�ڵ�E��AF��DC�ڵ�F��AE=AF��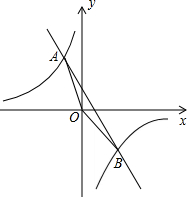 ��ͼ������������y=$\frac{k-1}{x}$��k��0����һ�κ���y=kx+b�ཻ��A��B���㣬����A������Ϊ��-1��7����
��ͼ������������y=$\frac{k-1}{x}$��k��0����һ�κ���y=kx+b�ཻ��A��B���㣬����A������Ϊ��-1��7����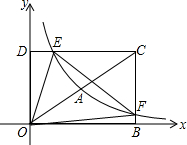 ��ͼ����ƽ��ֱ������ϵ�У���֪�ı���DOBC�Ǿ��Σ���D��0��2����B��3��0����������������y=-$\frac{{k}_{1}}{x}$��x��0����ͼ���߶�OC���е�A����DC�ڵ�E����BC�ڵ�F����ֱ��EF�Ľ���ʽΪy=k2x+b��
��ͼ����ƽ��ֱ������ϵ�У���֪�ı���DOBC�Ǿ��Σ���D��0��2����B��3��0����������������y=-$\frac{{k}_{1}}{x}$��x��0����ͼ���߶�OC���е�A����DC�ڵ�E����BC�ڵ�F����ֱ��EF�Ľ���ʽΪy=k2x+b��