题目内容
 (1)计算:2-1+(π-3.14)0+sin60°-|-
(1)计算:2-1+(π-3.14)0+sin60°-|-
| ||
| 2 |
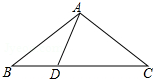
(2)如图,在△ABC中,AB=AC=10,sinC=
| 3 |
| 5 |
考点:解直角三角形,实数的运算,零指数幂,负整数指数幂,特殊角的三角函数值
专题:
分析:(1)分别根据0指数幂、负整数指数幂、特殊角的三角函数值即绝对值的性质计算出各数,再根据实数混合运算的法则进行计算即可;
(2)过点A作AE⊥BC于点E,根据等腰三角形的性质得出BE=CE,在Rt△ACE中根据AC=10,sin∠C=
,得出AE=6,由勾股定理求出CE的值,再由BD=BC-BD=BC-AC即可得出结论.
(2)过点A作AE⊥BC于点E,根据等腰三角形的性质得出BE=CE,在Rt△ACE中根据AC=10,sin∠C=
| 3 |
| 5 |
解答:(1)解:原式=
+1+
-
=
;
 (2)解:过点A作AE⊥BC于点E,
(2)解:过点A作AE⊥BC于点E,
∵AB=AC,
∴BE=CE,
在Rt△ACE中,AC=10,sin∠C=
,
∴AE=6,
∴CE=
=8,
∴BD=2CE=16,
∴BD=BC-BD=BC-AC=6.
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
=
| 3 |
| 2 |
 (2)解:过点A作AE⊥BC于点E,
(2)解:过点A作AE⊥BC于点E,∵AB=AC,
∴BE=CE,
在Rt△ACE中,AC=10,sin∠C=
| 3 |
| 5 |
∴AE=6,
∴CE=
| AC2-AE2 |
∴BD=2CE=16,
∴BD=BC-BD=BC-AC=6.
点评:本题考查的是解直角三角形,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
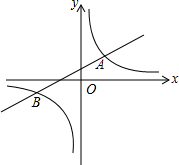 如图,一次函数y1=k1+2与反比例函数y2=
如图,一次函数y1=k1+2与反比例函数y2=| k2 |
| x |
| A、x<-8或0<x<4 |
| B、x>4或-8<x<0 |
| C、-8<x<4 |
| D、x<-8或x>4 |
三角形的周长为56cm,则它的三条中位线组成的三角形的周长是( )
| A、18cm | B、28cm |
| C、24cm | D、36cm |
 如图∠1=∠2,AB=10cm,AD:DB=2:3,那么AC=
如图∠1=∠2,AB=10cm,AD:DB=2:3,那么AC= 如图,长方体ABCD-A′B′C′D′中,有
如图,长方体ABCD-A′B′C′D′中,有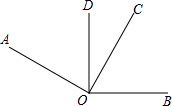 如图,∠AOC和∠BOD都是直角,∠DOC=28°,求出∠AOB的度数.
如图,∠AOC和∠BOD都是直角,∠DOC=28°,求出∠AOB的度数.