题目内容
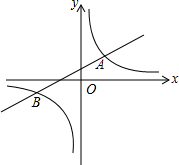如图，一次函数y1=k1+2与反比例函数y2=| k2 |
| x |
| A、x＜-8或0＜x＜4 |
| B、x＞4或-8＜x＜0 |
| C、-8＜x＜4 |
| D、x＜-8或x＞4 |
考点：反比例函数与一次函数的交点问题
专题：计算题
分析：根据反比例函数与一次函数的交点问题，先把B点坐标代入y2=
可计算出k2，确定反比例函数解析式，再把A（m，4）代入反比例函数解析式确定A点坐标，然后根据图象，找出一次函数图象在反比例函数图象上方所对应的自变量的取值范围即可．
| k2 |
| x |
解答：解：把B（-8，-2）代入y2=
得k2=-8×（-2）=16，
则分别漯河市解析式为y2=
，
把A（m，4）代入y2=
得4m=16，解得m=4，
所以A点坐标为（4，4），
当-8＜x＜0或x＞4时，y1＞y2．
故选B．
| k2 |
| x |
则分别漯河市解析式为y2=
| 16 |
| x |
把A（m，4）代入y2=
| 6 |
| x |
所以A点坐标为（4，4），
当-8＜x＜0或x＞4时，y1＞y2．
故选B．
点评：本题考查了反比例函数与一次函数的交点问题：求反比例函数与一次函数的交点坐标，把两个函数关系式联立成方程组求解，若方程组有解则两者有交点，方程组无解，则两者无交点．
练习册系列答案
相关题目
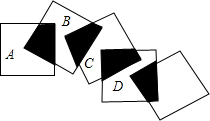如图，将五个边长都为2cm的正方形按如图所示摆放，点A、B、C、D分别是这四个正方形的对角线的交点，则图中四块阴影面积的总和是（ ）
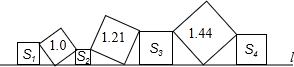如图，在直线l上依次摆放着七个正方形，已知斜放置的三个正方形的面积分别为1，1.21，1.44，正放置的四个正方形的面积为S1、S2、S3、S4，则S1+2S2+2S3+S4=
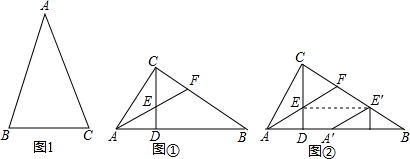
（1）计算：2-1+（π-3.14）0+sin60°-|-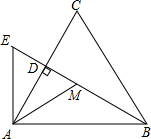
如图，已知△ABC是等边三角形，BD是AC上的高线．作AE⊥AB于点A，交BD的延长线于点E．取BE的中点M，连结AM．