题目内容
6.生活中有人喜欢把请人传送的便条折成图丁形状,折叠过程如图所示(阴影部分表示纸条反面),如果折成图丁形状的纸条宽 x cm,并且一端超出P点1cm,另一端超出P点2cm,那么折成的图丁所示的平面图形的面积为( )cm2.
| A. | $\frac{7}{2}{x^2}+3x$ | B. | $\frac{9}{2}{x^2}+3x$ | C. | $\frac{5}{2}{x^2}+3x$ | D. | 4x2+3x |
分析 根据折叠的性质可知,该图形的是由两个矩形和三个等腰直角三角形组合而成的,故只需求出矩形和等腰直角三角形的面积即可求解.
解答 解:如图,
根据折叠的性质可知:
AO=AC+CO=2+x,BP=1,
等腰直角三角形的直角边为x,
则S=AO•x+BP•x+3×$\frac{1}{2}$x2=2x+x2+x+$\frac{3}{2}$x2=$\frac{5}{2}$x2+3x.
故选C.
点评 本题考查了折叠的性质,难度一般,解答本题的关键是根据折叠的性质分析出各个图形的边长,求出各图形的面积.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
16.已知二次函数y=ax2+bx+c(a>0)的图象过点A(1,n),B(3,n),若点C(-1.y1),D(0,y2),E(6,y3)也在该二次函数图象上,则下列结论正确的是( )
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y3<y1<y2 | D. | y1<y3<y2 |
17.在某中学举行的“筑梦路上”演讲比赛中,八年级5名参赛选手的成绩分别为:90,93,89,90,88.关于这5名选手的成绩,下列说法正确的是( )
| A. | 平均数是89 | B. | 众数是93 | C. | 中位数是89 | D. | 方差是$\frac{14}{5}$ |
14. 如图,矩形ABCD的两条对角线相交于点O,∠AOB=120°,AD=2,点E是BC的中点,连结OE,则OE的长是( )
如图,矩形ABCD的两条对角线相交于点O,∠AOB=120°,AD=2,点E是BC的中点,连结OE,则OE的长是( )
 如图,矩形ABCD的两条对角线相交于点O,∠AOB=120°,AD=2,点E是BC的中点,连结OE,则OE的长是( )
如图,矩形ABCD的两条对角线相交于点O,∠AOB=120°,AD=2,点E是BC的中点,连结OE,则OE的长是( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 4 |
1.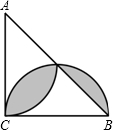 如图,△ABC 是等腰直角三角形,分别以直角边 AC,BC 为直径画弧,若 AB=2$\sqrt{2}$,则图中阴影部分的面积是( )
如图,△ABC 是等腰直角三角形,分别以直角边 AC,BC 为直径画弧,若 AB=2$\sqrt{2}$,则图中阴影部分的面积是( )
 如图,△ABC 是等腰直角三角形,分别以直角边 AC,BC 为直径画弧,若 AB=2$\sqrt{2}$,则图中阴影部分的面积是( )
如图,△ABC 是等腰直角三角形,分别以直角边 AC,BC 为直径画弧,若 AB=2$\sqrt{2}$,则图中阴影部分的面积是( )| A. | $\frac{π}{4}$-$\frac{1}{2}$ | B. | $\frac{3π}{4}$-$\frac{3}{2}$ | C. | $\frac{3π}{4}$-$\frac{3}{4}$ | D. | $\frac{π}{4}$+$\frac{3}{2}$ |
11.计算:$\sqrt{9}$=( )
| A. | 5 | B. | 2 | C. | 4 | D. | 3 |
18.估计5-$\sqrt{5}$介于( )
| A. | 4与1之间 | B. | 1与2之间 | C. | 2与3之间 | D. | 3与4之间 |
15.计算$\frac{1}{3}$-$\frac{1}{2}$的结果是( )
| A. | 6的倒数 | B. | 6的相反数 | C. | -6的绝对值 | D. | -6的倒数 |
16.下列调查中最适合采用普查的是( )
| A. | 调查某批次汽车的抗撞击能力 | |
| B. | 调查某班40名同学的视力情况 | |
| C. | 端午节期间,抚顺市食品安全检查部门调查市场上粽子的质量情况 | |
| D. | 调查某池塘中现有雨的数量 |