题目内容
5.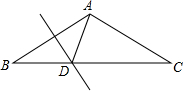 如图,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点D.
如图,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点D.(1)求∠ADC的度数;
(2)求证:DC=2DB.
分析 (1)根据等腰三角形两底角相等求出∠B,再根据线段垂直平分线上的点到两端点的距离相等可得AD=BD,根据等边对等角可得∠BAD=∠B,然后根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解;
(2)根据三角形的内角和得到∠DAC=90°,根据直角三角形的性质得到AD=$\frac{1}{2}$CD,∠BAD=30°,求得∠B=∠BAD,根据等腰三角形的性质即可得到结论.
解答 解:(1)∵AB=AC,∠BAC=120°,
∴∠B=$\frac{1}{2}$(180°-∠BAC)=$\frac{1}{2}$(180°-120°)=30°,
∵DE垂直平分AB,
∴AD=BD,
∴∠BAD=∠B=30°,
∴∠ADC=∠B+∠BAD=30°+30°=60°;
(2)∵∠ADC=60°,∠C=30°,
∴∠DAC=90°,
∴AD=$\frac{1}{2}$CD,∠BAD=30°,
∴∠B=∠BAD,
∴BD=AD,
∴DC=2DB.
点评 本题考查了线段垂直平分线上的点到两端点的距离相等的性质,等腰三角形的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质是解题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
 如图,AD∥BC,BO,CO分别平分∠ABC、∠DCB,∠A+∠D=m,求∠BOC的度数(用含m的代数式表示)
如图,AD∥BC,BO,CO分别平分∠ABC、∠DCB,∠A+∠D=m,求∠BOC的度数(用含m的代数式表示) 已知实数a、b在数轴上的位置如图所示,试化简:$\frac{a}{a-b}$$\sqrt{\frac{{a}^{2}b-2a{b}^{2}+{b}^{3}}{a}}$.
已知实数a、b在数轴上的位置如图所示,试化简:$\frac{a}{a-b}$$\sqrt{\frac{{a}^{2}b-2a{b}^{2}+{b}^{3}}{a}}$.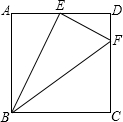 如图,在正方形ABCD中,AB=4,AE=2,DF=1,图中有几个直角三角形,说出你的理由.
如图,在正方形ABCD中,AB=4,AE=2,DF=1,图中有几个直角三角形,说出你的理由. 如图,将长为4,宽为2的长方形ABCD绕顶点A顺时针旋转90°到达AB′C′D′,图中的两段弧线分别是顶点C、D经过的路径,则阴影部分的面积为4.(π取3)
如图,将长为4,宽为2的长方形ABCD绕顶点A顺时针旋转90°到达AB′C′D′,图中的两段弧线分别是顶点C、D经过的路径,则阴影部分的面积为4.(π取3)