题目内容
20.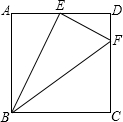 如图,在正方形ABCD中,AB=4,AE=2,DF=1,图中有几个直角三角形,说出你的理由.
如图,在正方形ABCD中,AB=4,AE=2,DF=1,图中有几个直角三角形,说出你的理由.
分析 共有四个,由正方形的性质可知△EAB,△BCF,△EDF都是直角三角形,再根据勾股定理的逆定理可证明△BEF也是直角三角形,问题得解.
解答 解:图中有4个直角三角形,理由如下:
∵四边形ABCD是正方形,
∴∠A=∠ABC=∠C=∠D=90°,
∴△EAB,△BCF,△EDF都是直角三角形,
∵AB=4,AE=2,
∴BE2=20,
∵DF=1,DE=4-AE=2,
∴EF2=5,
∵CF=4-DF=3,BC=4,
∴BF2=25,
∴BF2=EF2+BE2,
∴△BEF也是直角三角形,
∴图中有4个直角三角形.
点评 本题考查了正方形的性质以及勾股定理和其逆定理的运用,熟记正方形的性质是解题关键.

练习册系列答案
相关题目
11.下列各命题的逆命题成立的是( )
| A. | 三个内角相等的三角形是等边三角形 | |
| B. | 对顶角相等 | |
| C. | 三角形中,钝角所对的边最长 | |
| D. | 全等三角形的对应角相等 |
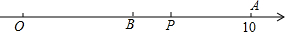 如图,数轴上的点O和A分别表示0和10,点P是线段OA上一动点,沿O→A→O以每秒2个单位的速度往返运动1次,B是线段OA的中点,设点P运动时间为t秒(0≤t≤10).
如图,数轴上的点O和A分别表示0和10,点P是线段OA上一动点,沿O→A→O以每秒2个单位的速度往返运动1次,B是线段OA的中点,设点P运动时间为t秒(0≤t≤10).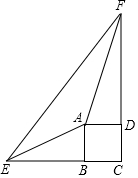 已知四边形ABCD是正方形,E、F分别在CB、CD的延长线上,∠EAF=135°.证明:BE+DF=EF.
已知四边形ABCD是正方形,E、F分别在CB、CD的延长线上,∠EAF=135°.证明:BE+DF=EF.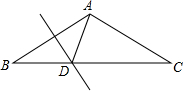 如图,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点D.
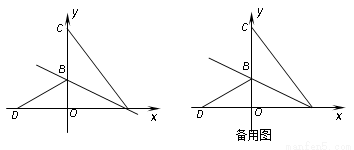
如图,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点D. 个单位长度的速度沿射线AB方向运动,过点P作PQ⊥AB,交x轴于点Q,PR∥AC交x轴于点R,设点P运动时间为t(秒),线段QR长为d,求d与t的函数关系式(不要求写出自变量t的取值范围);
个单位长度的速度沿射线AB方向运动,过点P作PQ⊥AB,交x轴于点Q,PR∥AC交x轴于点R,设点P运动时间为t(秒),线段QR长为d,求d与t的函数关系式(不要求写出自变量t的取值范围);