题目内容
13. 已知实数a、b在数轴上的位置如图所示,试化简:$\frac{a}{a-b}$$\sqrt{\frac{{a}^{2}b-2a{b}^{2}+{b}^{3}}{a}}$.
已知实数a、b在数轴上的位置如图所示,试化简:$\frac{a}{a-b}$$\sqrt{\frac{{a}^{2}b-2a{b}^{2}+{b}^{3}}{a}}$.
分析 利用实数在数轴的位置判断a,b,a-b的符号,再进一步化简合并即可.
解答 解:∵根据数轴可知:b>a>0,
∴a-b<0,
∴$\frac{a}{a-b}$$\sqrt{\frac{{a}^{2}b-2a{b}^{2}+{b}^{3}}{a}}$
=$\frac{a}{a-b}$$\sqrt{\frac{b({a}^{2}-2ab+{b}^{2})}{a}}$
=$\frac{a}{a-b}$$\frac{\sqrt{ab(a-b)^{2}}}{a}$
=$\frac{a}{a-b}$$\frac{-(a-b)\sqrt{ab}}{a}$
=-$\sqrt{ab}$.
点评 此题考查实数与数轴,绝对值的意义,二次根式的化简,正确判定字母与算式符号是解决问题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
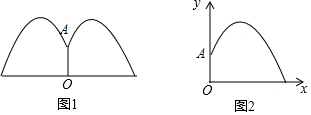 公园里有一个圆形喷水池,在水池中央垂直于水面安装一个花形柱子OA,O恰好在水面中心,布置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA任意平面上的抛物线如图1所示,建立直角坐标系如图2,水流喷出的高度(m)与水面距离x(m)之间的函数关系式是y=a(x-h)2+k,且OA=1.25m,水柱在离OA为1m处到时达最大高度2.25m,请回答下列问题:
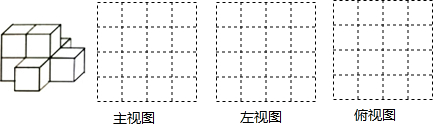
公园里有一个圆形喷水池,在水池中央垂直于水面安装一个花形柱子OA,O恰好在水面中心,布置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA任意平面上的抛物线如图1所示,建立直角坐标系如图2,水流喷出的高度(m)与水面距离x(m)之间的函数关系式是y=a(x-h)2+k,且OA=1.25m,水柱在离OA为1m处到时达最大高度2.25m,请回答下列问题: 如图,小方格是边长为1的正方形,则四边形ABCD的周长为15+3$\sqrt{5}$+$\sqrt{26}$.
如图,小方格是边长为1的正方形,则四边形ABCD的周长为15+3$\sqrt{5}$+$\sqrt{26}$.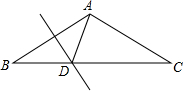 如图,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点D.
如图,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点D.