题目内容
16．
如图，AD∥BC，BO，CO分别平分∠ABC、∠DCB，∠A+∠D=m，求∠BOC的度数（用含m的代数式表示）
分析 根据四边形的内角和定理，可得出∠ABC+∠BCD，再由角平分线的性质，求得∠BOC．
解答 解：∵∠A+∠D=m，
∴∠ABC+∠BCD=360°-m，
∵BO、CO分别平分∠ABC、∠DCB，
∴∠OBC+∠OCB=180°-$\frac{1}{2}$m，
∴∠BOC=180°-（180°-$\frac{1}{2}$m）=$\frac{1}{2}$m．
点评 本题考查了四边形的内角和定理以及角平分线的性质，关键是根据四边形的内角和定理解答．
练习册系列答案
相关题目
如图，AC是?ABCD的对角线，点E、F在AC上，且四边形EBFD也是平行四边形，求证：AE=CF（思考不用全等的方法）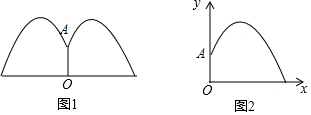
公园里有一个圆形喷水池，在水池中央垂直于水面安装一个花形柱子OA，O恰好在水面中心，布置在柱子顶端A处的喷头向外喷水，水流在各个方向上沿形状相同的抛物线路径落下，且在过OA任意平面上的抛物线如图1所示，建立直角坐标系如图2，水流喷出的高度（m）与水面距离x（m）之间的函数关系式是y=a（x-h）2+k，且OA=1.25m，水柱在离OA为1m处到时达最大高度2.25m，请回答下列问题：
11．下列各命题的逆命题成立的是（ ）
| A． | 三个内角相等的三角形是等边三角形 | |
| B． | 对顶角相等 | |
| C． | 三角形中，钝角所对的边最长 | |
| D． | 全等三角形的对应角相等 |
如图，小方格是边长为1的正方形，则四边形ABCD的周长为15+3$\sqrt{5}$+$\sqrt{26}$．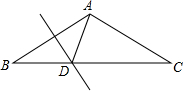
如图，AB=AC，∠BAC=120°，AB的垂直平分线交BC于点D．